题目内容
(1)如图,一次函数y=- x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.(2)我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?

【答案】分析:(1)作CD⊥x轴于点D,易证△ABO≌△CAD,即可求得AD,CD的长,则C的坐标即可求解;利用待定系数法即可求得直线BC的解析式;
(2)设文学书的单价是x元/本,则科普书的单价是x+4元/本,然后根据用12000元购进的科普书与用8000元购进的文学书本数相等,即可列出方程,从而求解.
解答: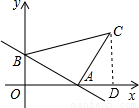 解:(1)一次函数y=-
解:(1)一次函数y=- x+2中,令x=0得:y=2;
x+2中,令x=0得:y=2;
令y=0,解得x=3.
则A的坐标是(3,0),B的坐标是(0,2).
作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO
又∵AB=AC,∠BOA=∠CDA=90°
∴△ABO≌△CAD,
∴AD=BO=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
设BC的解析式是y=kx+b,
根据题意得: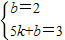 ,
,
解得: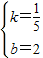 .
.
则BC的解析式是:y= x+2.
x+2.
(2)设文学书的单价是x元/本.
依题意得: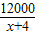 =
=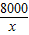
解得:x=8,经检验x=8是方程的解,并且符合题意.
x+4=12.
所以,去年购进的文学书和科普书的单价分别是8元和12元.
②设购进文学书550本后至多还能购进y本科普书.
依题意得550×8+12y≤10000,解得y≤466 ,
,
由题意取最大整数解,y=466.
所以,至多还能够进466本科普书.
点评:本题考查了待定系数法求直线的解析式,以及列方程解应用题,正确理解题目中的相等关系以及不等关系是关键.
(2)设文学书的单价是x元/本,则科普书的单价是x+4元/本,然后根据用12000元购进的科普书与用8000元购进的文学书本数相等,即可列出方程,从而求解.
解答:
 解:(1)一次函数y=-
解:(1)一次函数y=- x+2中,令x=0得:y=2;
x+2中,令x=0得:y=2;令y=0,解得x=3.
则A的坐标是(3,0),B的坐标是(0,2).
作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO
又∵AB=AC,∠BOA=∠CDA=90°
∴△ABO≌△CAD,
∴AD=BO=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
设BC的解析式是y=kx+b,
根据题意得:
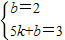 ,
,解得:
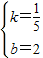 .
.则BC的解析式是:y=
 x+2.
x+2.(2)设文学书的单价是x元/本.
依题意得:
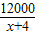 =
=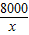
解得:x=8,经检验x=8是方程的解,并且符合题意.
x+4=12.
所以,去年购进的文学书和科普书的单价分别是8元和12元.
②设购进文学书550本后至多还能购进y本科普书.
依题意得550×8+12y≤10000,解得y≤466
 ,
,由题意取最大整数解,y=466.
所以,至多还能够进466本科普书.
点评:本题考查了待定系数法求直线的解析式,以及列方程解应用题,正确理解题目中的相等关系以及不等关系是关键.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数