题目内容
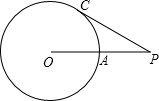已知：如图，⊙O半径为5，PC切⊙O于点C，PO交⊙O于点A，PA=4，那么PC的长等于（ ）| A、6 | ||
B、2
| ||
C、2
| ||
D、2
|
分析：延长AO交⊙O于B，由切割线定理可得PC2=PA•PB，进而求出PC的长．
解答：
解：延长AO交⊙O于B，
则AB=2OA=10；
由切割线定理得：PC2=PA•PB；
则有：PC2=4×（10+4）=56，
解得：PC=2
；
故选D．
解：延长AO交⊙O于B，则AB=2OA=10；
由切割线定理得：PC2=PA•PB；
则有：PC2=4×（10+4）=56，
解得：PC=2
| 14 |
故选D．
点评：此题主要考查的是切割线定理的应用．
练习册系列答案
阅读快车系列答案
相关题目
于点A、B，点A的坐标为（
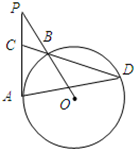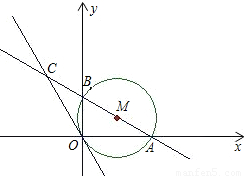
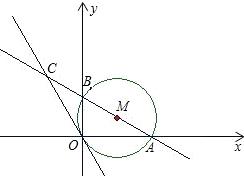
23、已知：如图，⊙O半径为6．过⊙O外一点P作⊙O的切线PA，A为切点，∠OPA=30°．过PO与⊙O的交点B作直线BC交PA于点C，交⊙O于点D．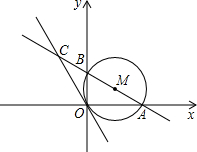
已知，如图，半径为1的⊙M经过直角坐标系的原点O，且与x轴、y轴分别交于点A、B，点A的坐标为（
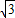，0），⊙M的切线OC与直线AB交于点C．