题目内容
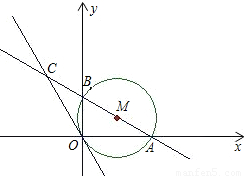
已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交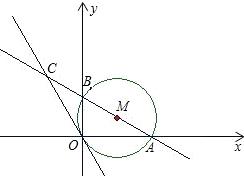 于点A、B,点A的坐标为(
于点A、B,点A的坐标为(| 3 |
(1)求点B的坐标;
(2)求∠ACO的度数;
(3)求直线OC的函数解析式.
分析:(1)已知了圆的半径就知道了AB的长,已知了A的坐标,就知道了OA的长,根据勾股定理就能求出OB的长,因此B点的坐标就求出来了;
(2)可通过构建三角形来求解.连接OM,则MO⊥OC,三角形MOC和AOB中,已知了一组直角,在(1)中我们求得OB=OM=1,因此∠OMB=∠OBM,因此两三角形全等,那么∠OAC=∠OCA,在(1)中求出了OB的值,有AB的值,那么∠OAC的度数就不难求出了,也就求出了∠OCA的度数;
(3)关键是求出C的坐标,可通过构建三角形来求解.由(2)得出的全等三角形我们知道:OC=OA=
,∠OAC=∠OCA=30°,因此∠COD=60°,因此可求出CD,OD的长,也就求出了C的坐标,可用待定系数法求出正比例函数的函数式.
(2)可通过构建三角形来求解.连接OM,则MO⊥OC,三角形MOC和AOB中,已知了一组直角,在(1)中我们求得OB=OM=1,因此∠OMB=∠OBM,因此两三角形全等,那么∠OAC=∠OCA,在(1)中求出了OB的值,有AB的值,那么∠OAC的度数就不难求出了,也就求出了∠OCA的度数;
(3)关键是求出C的坐标,可通过构建三角形来求解.由(2)得出的全等三角形我们知道:OC=OA=
| 3 |
解答: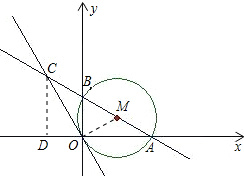 解:(1)AB=2,OA=
解:(1)AB=2,OA=
OB=
=1,
点B的坐标(0,1);
(2)连接OM,
由(1)得:OB=1=OM,∠OBA=∠OMB,
又∵∠MOC=∠AOB=90°,
∴Rt△AOB≌Rt△COM,
∵OB=1,AB=2,
∴∠BAO=30°,
∴∠ACO=∠BAO=30°;
(3)由(2)知:OC=OA=
,∠OAC=∠OCA=30°,
过C作CD⊥OA交x轴于D,
那么在Rt△OCD中,∠COD=60°,
∴OD=
,CD=
,
∴C点的坐标应是(-
,
),
设OC所在的直线为y=kx,
-
k=
,
k=-
,
∴函数的解析式为:y=-
x.
 解:(1)AB=2,OA=
解:(1)AB=2,OA=| 3 |
22-(
|
点B的坐标(0,1);
(2)连接OM,
由(1)得:OB=1=OM,∠OBA=∠OMB,
又∵∠MOC=∠AOB=90°,
∴Rt△AOB≌Rt△COM,
∵OB=1,AB=2,
∴∠BAO=30°,
∴∠ACO=∠BAO=30°;
(3)由(2)知:OC=OA=
| 3 |
过C作CD⊥OA交x轴于D,
那么在Rt△OCD中,∠COD=60°,
∴OD=
| ||
| 2 |
| 3 |
| 2 |
∴C点的坐标应是(-
| ||
| 2 |
| 3 |
| 2 |
设OC所在的直线为y=kx,
-
| ||
| 2 |
| 3 |
| 2 |
k=-
| 3 |
∴函数的解析式为:y=-
| 3 |
点评:本题的解题关键是通过直角三角形求出线段的长进而得出点的坐标.

练习册系列答案
相关题目
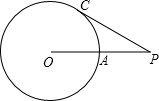 已知:如图,⊙O半径为5,PC切⊙O于点C,PO交⊙O于点A,PA=4,那么PC的长等于( )
已知:如图,⊙O半径为5,PC切⊙O于点C,PO交⊙O于点A,PA=4,那么PC的长等于( )| A、6 | ||
B、2
| ||
C、2
| ||
D、2
|
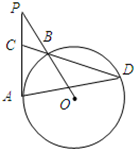 23、已知:如图,⊙O半径为6.过⊙O外一点P作⊙O的切线PA,A为切点,∠OPA=30°.过PO与⊙O的交点B作直线BC交PA于点C,交⊙O于点D.
23、已知:如图,⊙O半径为6.过⊙O外一点P作⊙O的切线PA,A为切点,∠OPA=30°.过PO与⊙O的交点B作直线BC交PA于点C,交⊙O于点D.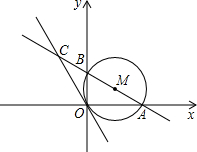 已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(
已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(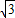 ,0),⊙M的切线OC与直线AB交于点C.
,0),⊙M的切线OC与直线AB交于点C.