题目内容
【题目】甲、乙两名运动员进行长跑训练,两人距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
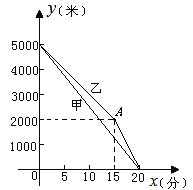
(1)他们在进行 米的长跑训练,在0<![]() <15的时间内,速度较快的人是 (填“甲”或“乙”);
<15的时间内,速度较快的人是 (填“甲”或“乙”);
(2)求乙距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(3)当![]() =15时,两人相距多少米?
=15时,两人相距多少米?
(4)在15<![]() <20的时间段内,求两人速度之差.
<20的时间段内,求两人速度之差.
【答案】(1)5000;甲;(2)![]() ;(3)750米;(4)150米/分.
;(3)750米;(4)150米/分.
【解析】
(1)根据x=0时,y=5000可知,他们在进行5000米的长跑训练,在0<![]() <15的时间内,
<15的时间内,![]() ,所以甲跑的快;
,所以甲跑的快;
(2)分段求解析式,在0<![]() <15的时间内,由点(0,5000),(15,2000)来求解析式;在15≤
<15的时间内,由点(0,5000),(15,2000)来求解析式;在15≤![]() ≤20的时间内,由点(15,2000),(20,0)来求解析式;
≤20的时间内,由点(15,2000),(20,0)来求解析式;
(3)根据题意求得甲的速度为250米/分,然后计算甲距离终点的路程,再计算他们的距离;
(4)在15<![]() <20的时间段内,求得乙的速度,然后计算他们的速度差.
<20的时间段内,求得乙的速度,然后计算他们的速度差.
(1)根据图象信息可知,他们在进行5000米的长跑训练,
在0<x<15的时间段内,直线y甲的倾斜程度大于直线y乙的倾斜程度,所以甲的速度较快;
(2)①在0<![]() <15内,设y=kx+b,
<15内,设y=kx+b,
把(0,5000),(15,2000)代入解析式,解得k=-200,b=5000,
所以y=-200x+5000;
②在15≤![]() ≤20内,设
≤20内,设![]() ,
,
把(15,2000),(20,0)代入解析式,解得![]() ,
,![]() ,
,
所以y=-400x+8000,
所以乙距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系式为:
(分)之间的函数关系式为:![]() ;
;
(3)甲的速度为5000÷20=250(米/分),250×15=3750米,距终点5000-3750=1250米,
此时乙距终点2000米,所以他们的距离为2000-1250=750米;
(4)在15<![]() <20的时间段内,乙的速度为2000÷5=400米/分,甲的速度为250米/分,所以他们的速度差为400-250=150米/分.
<20的时间段内,乙的速度为2000÷5=400米/分,甲的速度为250米/分,所以他们的速度差为400-250=150米/分.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】我校初三某班 50 名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)填空:a= ,b= ;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“立定跳远”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有 3 名男生、2 名女生,为了了解学生的训练效果,从这 5 名学生中随机抽取两名学生进行推铅球测试,请用列表法或树形图法求所抽取的两名学生中至多有一名男生的概率.