��Ŀ����
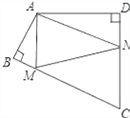
����Ŀ����ͼ���߳�Ϊ2�ĵȱ���ABC�ڽ�����O����ABC��Բ��O˳ʱ����ת�õ���A��B��C����A��C���ֱ��ڵ�E��D������ת��Ϊa��0����a��360������
��1����a= ʱ����A���BC������ABC������ת�����еĵ�һ����ȫ�غϣ�
��2����a=60������ͼ1������ͼ
A�������ĶԳ�ͼ�ε�������Գ�ͼ�� B������Գ�ͼ�ε��������ĶԳ�ͼ��
C��������Գ�ͼ���������ĶԳ�ͼ�� D���Ȳ�����Գ�ͼ��Ҳ�������ĶԳ�ͼ��
��3����ͼ2����0����a��120��ʱ����ADE���ܳ��Ƿ�ᷢ���仯������仯����˵�����ɣ�������仯����������ܳ���
���𰸡�(1)��120����(2)��C��(3)��2.
��������
���������(1)������BO��CO������Բ�ĽǵĿɵ�a�Ķ������ɣ�(2)��������Գ�ͼ�������ĶԳ�ͼ�εĶ����жϼ��ɣ�(3)������AA'�����õ��ҶԵȻ���ɣ�
���������(1)������BO��CO����ͼ1��

��BOC=![]() �����Ե�a=120��ʱ����A���BC������ABC������ת�����еĵ�һ����ȫ�غϣ�
�����Ե�a=120��ʱ����A���BC������ABC������ת�����еĵ�һ����ȫ�غϣ�
(2)���۲�ͼ1���ɵø�ͼ������Գ�ͼ���������ĶԳ�ͼ�Σ���ѡC��
(3)����ADE���ܳ����䣬
��ͼ2������AA'��

��AB=A'C'�� ��![]() ����
����![]() �����BAA'=��AA'C�� ��EA=EA���� ͬ��DA=DC'��
�����BAA'=��AA'C�� ��EA=EA���� ͬ��DA=DC'��
���ADE���ܳ�=EA+ED+DA=EA'+ED+DC'=A'C'=2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�̵���Ҫ�����ס���������Ʒ��180��������ۺ��ۼ��������ע������=�ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 14 | 35 |
�ۼۣ�Ԫ/���� | 20 | 43 |
��1�����̵�ƻ�������������Ʒ���ܻ���1240Ԫ���ʼס���������ƷӦ�ֱ����ټ���
��2�����̵�ƻ�Ͷ���ʽ�����5040Ԫ����������������Ʒ���������1312Ԫ���������ļ��ֹ�����������ֱ��д�����л������Ĺ���������