题目内容
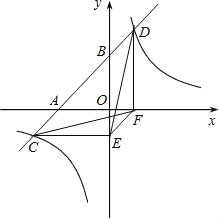
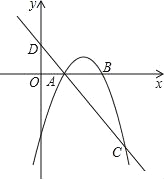
【题目】如图，已知抛物线y=ax2+bx-3（a≠0）与x轴交于A，B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，-3）．
（1）求抛物线解析式；
（2）点M是（1）中抛物线上一个动点，且位于直线AC的上方，试求△ACM的最大面积以及此时点M的坐标；
（3）抛物线上是否存在点P，使得△PAC是以AC为直角边的直角三角形？如果存在，求出P点的坐标；如果不存在，请说明理由．
【答案】（1）y=-x2+4x-3；（2）
，M（
，
）；（3）（-1，-8）或（2，1）.
【解析】
试题分析：（1）代入A，C两点，列出方程，解得a，b即可；
（2）设M（a，-a2+4a-3），求出直线直线AC的解析式为：y=1-x，过M作x轴的垂线交AC于N，则N（a，1-a），即有三角形ACM的面积为△AMN和△CMN的面积之和，化简运用二次函数的最值，即可得到；
（3）讨论当∠ACP=90°，当∠CAP=90°，运用直线方程和抛物线方程求交点即可．
试题解析：（1）由于A点的坐标是（1，0），C点坐标是（4，-3），
则a+b-3=0，且16a+4b-3=-3，
解得，a=-1，b=4，
即抛物线的解析式为：y=-x2+4x-3；
（2）设M（a，-a2+4a-3），
设直线AC的解析式为y=kx+b，
根据题意得：
，
解得：
，
∴直线AC的解析式为：y=1-x，
过M作x轴的垂线交AC于N，
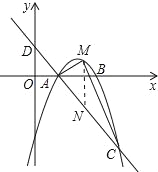
如图所示：则N（a，1-a），
即有三角形ACM的面积为△AMN与△CMN的面积之和，即为
（a-1+4-a）（-a2+4a-3-1+a）
=
（-a2+5a-4），
当a=时，面积取得最大，且为，
此时M（，）；
（3）存在，理由如下：
当∠ACP=90°，即有此时CP：y=x-7，
由CP解析式和抛物线解析式得：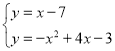
，
解得：
，或
（不合题意舍去），
∴P（-1，-8）；
当∠CAP=90°，由AC的斜率为-1，即有AP的斜率为1，
此时AP：y=x-1，
由AP解析式和抛物线解析式得：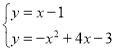
，
解得：
，或
，（不合题意舍去），
∴P（2，1）．
故存在点P，且为（-1，-8）或（2，1），使得△PAC是以AC为直角边的直角三角形．
