题目内容
【题目】如图,直线l1的解析表达式为y=﹣3x+3,且l1与x轴交于点D.直线l2经过点A、B,直l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)在直线l2上存在异于点C的另一个点P,使得△ADP与△ADC的面积相等,求P点的坐标.
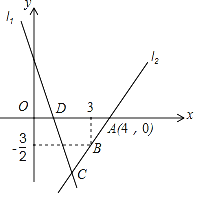
【答案】(1)、(1,0);(2)、y=1.5x﹣6;(3)、(6,3).
【解析】
试题分析:(1)、利用x轴上点的坐标特征求D点坐标; (2)、利用待定系数法确定直线l2的解析式;
(3)、由于△ADP与△ADC的面积相等,根据三角形面积公式得到点P与点C到AD的距离相等,则P点的纵坐标为3,对于函数y=![]() x﹣6,计算出函数值为3所对应的自变量的值即可得到P点坐标.
x﹣6,计算出函数值为3所对应的自变量的值即可得到P点坐标.
试题解析:(1)、把y=0代入y=﹣3x+3,得 ﹣3x+3=0, 解得x=1, 所以D点坐标为(1,0);
(2)、设直线l2的解析式为y=kx+b, 把A(4,0)、B(3,﹣![]() )代入得
)代入得 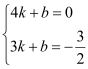 , 解得
, 解得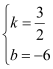 ,
,
所以直线l2的解析式为y=![]() x﹣6;
x﹣6;
(3)、解方程组 ,得
,得 ![]() , 即C(2,﹣3), 因为点P与点C到AD的距离相等,
, 即C(2,﹣3), 因为点P与点C到AD的距离相等,
所以P点的纵坐标为3, 当y=3时,![]() x﹣6=3, 解得x=6, 所以P点坐标为(6,3).
x﹣6=3, 解得x=6, 所以P点坐标为(6,3).

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
【题目】在开展“好书伴我成长”的读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.