题目内容
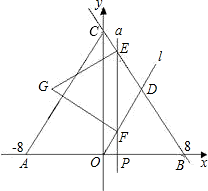
如图,在平面坐标系中有一正三角形ABC,A(-8,0)、B(8,0),直线l经过原点O及BC的中点D,另一动直线a平行于y轴,从原点出发,以每秒1个单位长度的速度沿x轴向右平移,直线a分别交线段BC、直线l于点E、F,以EF为边向左侧作等边△EFG,设△EFG与△ABC重叠部分的面积为S(平方单位),当点G落在y轴上时,a停止运动,设直线a的运动时间为t(秒).(1)直接写出:C点坐标______
【答案】分析:(1)由勾股定理求出OC,得到C的坐标,根据三角形的中位线定理得出D的坐标,设直线l的解析式是y=kx,把D的坐标代入即可求出解析式;
(2)OP=t,则BP=8-t,根据勾股定理求出EP和FP即可求出EF;
(3)当EF在y轴时,t=0;当G落在y轴时,a停止运动,此时t=3即可得到t的范围;当G落在AC边上时,t=2,当0≤t<2时,重叠部分为四边形,根据三角形的面积公式即可求出S=-3 t2+24
t2+24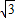 ;当2≤t≤3时,重叠部分就是三角形GEF,根据三角形的面积公式即可求出S.
;当2≤t≤3时,重叠部分就是三角形GEF,根据三角形的面积公式即可求出S.
解答:解:(1)∵等边△ABC,AC=AB=8+8=16,
∴由勾股定理得:OC=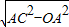 =
=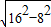 =8
=8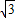 ,
,
∴C点坐标(0,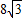 ),
),
设直线l的解析式是y=kx(k≠0),
过D作DM⊥x轴,交x轴于点M,
∵D为BC的中点,DM∥CO,
∴M为OB的中点,又OC=8 ,OB=8,
,OB=8,
∴DM=4 ,OM=4,
,OM=4,
∴D的坐标为(4,4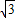 ),
),
把D点的坐标代入得:k= ,
,
直线l的解析式:y= x,
x,
故答案为:(0,8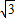 ),y=
),y= x.
x.
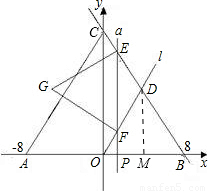
(2)解:OP=t,则BP=8-t,
在Rt△OPF中,∠FPO=60°∴PF=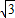 t,
t,
在Rt△EPB中,∠PBE=60°∴EP=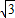 (8-t),
(8-t),
∴EF=EP-FP=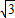 (8-t)-
(8-t)- t=8
t=8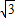 -2
-2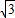 t,
t,
答:用含t的代数式表示线段EF为:8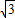 -2
-2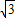 t.
t.
(3)解:当EF在y轴时,t=0;
当G落在y轴时,a停止运动,此时t=3
∴t的取值范围是:0≤t≤3,
当G落在AC边上时,t=2,
当0≤t<2时,重叠部分为四边形,S=-3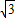 t2+24
t2+24 ,
,
当2≤t≤3时,重叠部分就是三角形GEF,S=S△GEF=3 (4-t)2.
(4-t)2.
答:S关于t的函数关系式是S=-3 t2+24
t2+24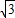 或S=3
或S=3 (4-t)2,t的取值范围是0≤t≤3.
(4-t)2,t的取值范围是0≤t≤3.
点评:本题主要考查对三角形的面积,一次函数的性质,用待定系数法求正比例函数的解析式,三角形的中位线定理,勾股定理等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,题型较好,难度适中.
(2)OP=t,则BP=8-t,根据勾股定理求出EP和FP即可求出EF;
(3)当EF在y轴时,t=0;当G落在y轴时,a停止运动,此时t=3即可得到t的范围;当G落在AC边上时,t=2,当0≤t<2时,重叠部分为四边形,根据三角形的面积公式即可求出S=-3
 t2+24
t2+24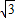 ;当2≤t≤3时,重叠部分就是三角形GEF,根据三角形的面积公式即可求出S.
;当2≤t≤3时,重叠部分就是三角形GEF,根据三角形的面积公式即可求出S.解答:解:(1)∵等边△ABC,AC=AB=8+8=16,
∴由勾股定理得:OC=
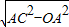 =
=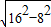 =8
=8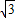 ,
,∴C点坐标(0,
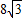 ),
),设直线l的解析式是y=kx(k≠0),
过D作DM⊥x轴,交x轴于点M,
∵D为BC的中点,DM∥CO,
∴M为OB的中点,又OC=8
 ,OB=8,
,OB=8,∴DM=4
 ,OM=4,
,OM=4,∴D的坐标为(4,4
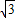 ),
),把D点的坐标代入得:k=
 ,
,直线l的解析式:y=
 x,
x,故答案为:(0,8
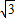 ),y=
),y= x.
x.
(2)解:OP=t,则BP=8-t,
在Rt△OPF中,∠FPO=60°∴PF=
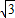 t,
t,在Rt△EPB中,∠PBE=60°∴EP=
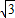 (8-t),
(8-t),∴EF=EP-FP=
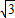 (8-t)-
(8-t)- t=8
t=8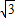 -2
-2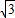 t,
t,答:用含t的代数式表示线段EF为:8
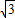 -2
-2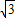 t.
t.(3)解:当EF在y轴时,t=0;
当G落在y轴时,a停止运动,此时t=3
∴t的取值范围是:0≤t≤3,
当G落在AC边上时,t=2,
当0≤t<2时,重叠部分为四边形,S=-3
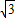 t2+24
t2+24 ,
,当2≤t≤3时,重叠部分就是三角形GEF,S=S△GEF=3
 (4-t)2.
(4-t)2.答:S关于t的函数关系式是S=-3
 t2+24
t2+24 或S=3
或S=3 (4-t)2,t的取值范围是0≤t≤3.
(4-t)2,t的取值范围是0≤t≤3.点评:本题主要考查对三角形的面积,一次函数的性质,用待定系数法求正比例函数的解析式,三角形的中位线定理,勾股定理等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,题型较好,难度适中.

练习册系列答案
相关题目
 16、如图,在平面坐标系中,ABCO为正方形,已知点B的坐标为(4,4),点P的坐标为(3,3),当三角板直角顶点与P重合时,一条直角边与x轴交于点E,另一条直角边与y轴交于点F,在三角板绕点P旋转过程中,若△POE为等腰三角形,则点F的坐标为
16、如图,在平面坐标系中,ABCO为正方形,已知点B的坐标为(4,4),点P的坐标为(3,3),当三角板直角顶点与P重合时,一条直角边与x轴交于点E,另一条直角边与y轴交于点F,在三角板绕点P旋转过程中,若△POE为等腰三角形,则点F的坐标为
 (2013•长沙)如图,在平面坐标系中,直线y=-x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.
(2013•长沙)如图,在平面坐标系中,直线y=-x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.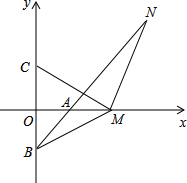 如图,在平面坐标系中,A(a,0),B(0,b),且a,b满足(a-4)2+
如图,在平面坐标系中,A(a,0),B(0,b),且a,b满足(a-4)2+