题目内容
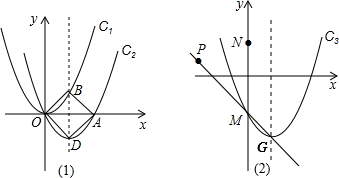
(2013•河池)已知:抛物线C1:y=x2.如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D.
(1)求抛物线C2的解析式;
(2)探究四边形ODAB的形状并证明你的结论;
(3)如图(2),将抛物线C2向m个单位下平移(m>0)得抛物线C3,C3的顶点为G,与y轴交于M.点N是M关于x轴的对称点,点P(-
m,
m)在直线MG上.问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
(1)求抛物线C2的解析式;
(2)探究四边形ODAB的形状并证明你的结论;
(3)如图(2),将抛物线C2向m个单位下平移(m>0)得抛物线C3,C3的顶点为G,与y轴交于M.点N是M关于x轴的对称点,点P(-
| 4 |
| 3 |
| 1 |
| 3 |

分析:(1)设设抛物线C2的解析式为y=x2+bx,把A(2,0)代入求出b的值即可;
(2)四边形ODAB的形状为正方形,求出抛物线C2的顶点坐标D为(1,-1)和B的坐标为(1,1)进而证明四边形ODAB为菱形,再证明是正方形即可;
(3)当M、N、P、Q为顶点的四边形为平行四边形时有两种情况:①若MN是平行四边形的一条边②若MN是平行四边形的一条对角线,在分别讨论求出满足题意的m值即可.
(2)四边形ODAB的形状为正方形,求出抛物线C2的顶点坐标D为(1,-1)和B的坐标为(1,1)进而证明四边形ODAB为菱形,再证明是正方形即可;
(3)当M、N、P、Q为顶点的四边形为平行四边形时有两种情况:①若MN是平行四边形的一条边②若MN是平行四边形的一条对角线,在分别讨论求出满足题意的m值即可.
解答:解:(1)∵抛物线C2经过C1的顶点O,
∴设抛物线C2的解析式为y=x2+bx,
∵C2经过A(2,0),
∴4+2b=0,
解得:b=-2,
∴求抛物线C2的解析式为y=x2-2x;
(2)∵y=x2-2x=(x-1)2-1,
∴抛物线C2的顶点坐标D为(1,-1),
当x=1时,y=1,
∴点B的坐标为(1,1),
∴根据勾股定理得:OB=AB=OD=AD=
,
∴四边形ODAB是菱形,
又∵OA=BD=2,
∴四边形ODAB是正方形;
(3)∵抛物线C2向m个单位下平移(m>0)得抛物线C3,
∴抛物线C3的解析式为y=(x-1)2-1-m,
在y=(x-1)2-1-m中,令x=0,得y=-m,
∴M(0,-m),
∵点N是M关于x轴的对称点,
∴N(0,m),
∴MN=2m,
当M、N、P、Q为顶点的四边形为平行四边形时有两种情况:
①若MN是平行四边形的一条边,
由MN=PQ=2m和点P(-
m,
m)得Q(-
m,
m),
∵点Q在抛物线C3上,
∴
m=(-
m-1)2-1-m,
解得:m=
或m=0(舍去),
②若MN是平行四边形的一条对角线,由平行四边形的中心对称得Q(
m,-
m)
∵点Q在抛物线C3上,
∴-
m=(
m-1)2-1-m,解得:m=
或m=0(舍去)
综上所述,当m=
或
时,
在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形.
∴设抛物线C2的解析式为y=x2+bx,
∵C2经过A(2,0),
∴4+2b=0,
解得:b=-2,
∴求抛物线C2的解析式为y=x2-2x;
(2)∵y=x2-2x=(x-1)2-1,
∴抛物线C2的顶点坐标D为(1,-1),
当x=1时,y=1,
∴点B的坐标为(1,1),
∴根据勾股定理得:OB=AB=OD=AD=
| 2 |
∴四边形ODAB是菱形,
又∵OA=BD=2,
∴四边形ODAB是正方形;
(3)∵抛物线C2向m个单位下平移(m>0)得抛物线C3,
∴抛物线C3的解析式为y=(x-1)2-1-m,
在y=(x-1)2-1-m中,令x=0,得y=-m,
∴M(0,-m),
∵点N是M关于x轴的对称点,
∴N(0,m),
∴MN=2m,
当M、N、P、Q为顶点的四边形为平行四边形时有两种情况:
①若MN是平行四边形的一条边,
由MN=PQ=2m和点P(-
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
∵点Q在抛物线C3上,
∴
| 7 |
| 3 |
| 4 |
| 3 |
解得:m=
| 3 |
| 8 |
②若MN是平行四边形的一条对角线,由平行四边形的中心对称得Q(
| 4 |
| 3 |
| 1 |
| 3 |
∵点Q在抛物线C3上,
∴-
| 1 |
| 3 |
| 4 |
| 3 |
| 15 |
| 8 |
综上所述,当m=
| 3 |
| 8 |
| 15 |
| 8 |
在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形.
点评:本题考查了二次函数的平移、二次函数的顶点坐标的求法、平行四边形的判定和性质以及菱形、正方形的判定和性质,用到的知识点还有一元二次方程的解法以及分类讨论的数学思想,题目的综合性很强,难度很大.

练习册系列答案
相关题目
 (2013•河池)如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.
(2013•河池)如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.