题目内容
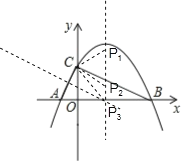
【题目】如图,在平面直角坐标系中,抛物线![]() 与坐标轴分别交于点A、点B、点C,并且∠ACB=90,AB=10.
与坐标轴分别交于点A、点B、点C,并且∠ACB=90,AB=10.
(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)证明见解析;(2)y=-![]() ;(3)(3,4+
;(3)(3,4+![]() ),(3,4-
),(3,4-![]() ),(3,0).
),(3,0).
【解析】试题分析:(1)根据余角的性质得到![]() ,根据相似三角形的判定定理即可得到结论;
,根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到![]() 得到
得到![]() 解方程组即可得到结论;
解方程组即可得到结论;
(3)设![]() ,根据两点间的距离得到
,根据两点间的距离得到![]()
![]()
![]() ①当
①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,解方程即可得到结论.
时,解方程即可得到结论.
试题解析:(1) ![]()
![]()
∴∠CAO=∠BCO,
∴△OAC∽△OCB;
(2)∵在![]() 中,当x=0,y=4,
中,当x=0,y=4,
∴OC=4,
∵△OAC∽△OCB,
∴![]() ,
,
![]()
∴OB=2或OB=8,
∴A(2,0),B(8,0),
将上述坐标代入![]() 得
得
![]()
解得
∴所求作的解析式为: ![]()
(3)存在,∵![]()
∴抛物线的对称轴为:直线x=3,
∴设P(3,n),
∵A(2,0),C(0,4),
![]()
![]()
![]()
∵△PAC为等腰三角形,
①当AC=AP时,即![]()
此方程无实数根,这种情况不存在;
②当AC=CP时,即![]()
解得: ![]()
③当AP=CP时,即![]()
解得:n=0,
∴P ![]() ,
, ![]() .
.

【题目】疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(只) | 2000 | 1500 | 1200 | 1000 |
(1)猜测并确定y与x之间的函数关系式;
(2)设经营此口罩的销售利润为W元,求出W与x之间的函数关系式?
(3)若物价局规定此口罩的售价最高不能超过10元/只,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.






