题目内容
【题目】![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 平分
平分![]() .
.
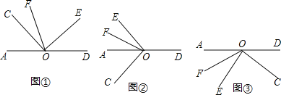
![]() 如图①,
如图①,![]() 与
与![]() 的数量关系为________,
的数量关系为________,![]() 和
和![]() 的数量关系为_________;
的数量关系为_________;
![]() 若将
若将![]() 绕点
绕点![]() 旋转至图②的位置,
旋转至图②的位置,![]() 依然平分
依然平分![]() ,请写出
,请写出![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
![]() 若将
若将![]() 绕点
绕点![]() 旋转至图③的位置,射线
旋转至图③的位置,射线![]() 依然平分
依然平分![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
【答案】(1)互余;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据已知条件和图形可知:∠COE=90°,∠COE+∠AOC+∠DOE=180°,从而可以得到∠AOC与∠DOE的数量关系;由射线OF平分∠AOE,∠AOC与∠DOE的数量关系,从而可以得到∠COF和∠DOE的数量关系;
(2)由图②,可以得到各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系;
(3)由图③和已知条件可以建立各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系.
(1)∵∠COE=90°,∠COE+∠AOC+∠DOE=180°,
∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,
∴∠AOF=∠EOF=![]() ∠AOE,
∠AOE,
∴∠COF=∠AOF-∠AOC=![]() ∠AOE-(90°-∠DOE)=
∠AOE-(90°-∠DOE)=![]() (180°-∠DOE)-90°+∠DOE=
(180°-∠DOE)-90°+∠DOE=![]() ∠DOE,
∠DOE,
故答案为:互余,∠COF=![]() ∠DOE;
∠DOE;
(2)![]() ;理由如下:
;理由如下:
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ;
;
(3)![]() ;理由如下:
;理由如下:
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴ ,
,
即![]() .
.

练习册系列答案
相关题目