题目内容
 如图,在△ABC中,∠CAB=90°,AB=3,AC=4,AD是∠CAB的平分线,AD交BC于D,求BD的长.
如图,在△ABC中,∠CAB=90°,AB=3,AC=4,AD是∠CAB的平分线,AD交BC于D,求BD的长.考点:角平分线的性质,勾股定理
专题:几何图形问题
分析:过C作CM∥AD,交BA延长线于M,求,AM=AC=4,根据平行线的性质得出
=
,即可求出答案.
| BD |
| CD |
| 3 |
| 4 |
解答: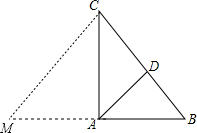
解:由勾股定理得:AB=
=5,
过C作CM∥AD,交BA延长线于M,
则∠M=∠DAB,∠ACM=∠CAD,
∵AD平分∠CAB,
∴∠DAB=∠CAD,
∴∠M=∠MCA,
∴AM=AC=4,
∵AB=3,CM∥AD,
∴
=
=
,
∴BD=
BC=
.

解:由勾股定理得:AB=
| 32+42 |
过C作CM∥AD,交BA延长线于M,
则∠M=∠DAB,∠ACM=∠CAD,
∵AD平分∠CAB,
∴∠DAB=∠CAD,
∴∠M=∠MCA,
∴AM=AC=4,
∵AB=3,CM∥AD,
∴
| BD |
| CD |
| AB |
| CM |
| 3 |
| 4 |
∴BD=
| 3 |
| 7 |
| 15 |
| 7 |
点评:本题考查了平行线分线段成比例定理,等腰三角形的性质和判定,勾股定理的应用,解此题的关键是求出
=
.
| BD |
| CD |
| 3 |
| 4 |

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 已知△ABC中,AE平分∠BAC,BC平分∠EBF,若AB=AC,求证:四边形BECF是菱形.
已知△ABC中,AE平分∠BAC,BC平分∠EBF,若AB=AC,求证:四边形BECF是菱形.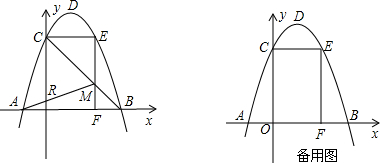
 如图,反比例函数
如图,反比例函数