题目内容
 如图,反比例函数y=-
如图,反比例函数y=-| k |
| x |
(1)求k的取值范围;
(2)当k取何值时,点A的纵坐标为3;
(3)在(2)的条件下,x取何值时,反比例函数y=-
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)反比例函数与一次函数的交点问题得到方程组
,消去y得到x2-2x-k=0,利用判别式的应义得到△=(-2)2-4(-k)≥0,然后解不等式即可;
(2)先根据一次函数解析式确定A点坐标,然后把A点坐标代入y=-
求出k即可;
(3)先解方程组
确定B点坐标为(3,-1),然后观察函数图象得到当-1<x<0或x>3时,反比例函数y=-
的图象都在一次函数y=-x+2的图象上方.
|
(2)先根据一次函数解析式确定A点坐标,然后把A点坐标代入y=-
| k |
| x |
(3)先解方程组
|
| k |
| x |
解答:解:(1)由
得x2-2x-k=0,
∴△=(-2)2-4(-k)≥0,解得k>-1,
∴k的取值范围为k>-1且k≠0;
(2)把y=3代入y=-x+2得-x+2=3,解得x=-1,
∴A点坐标为(-1,3),
把A(-1,3)代入y=-
得-k=-1×3,解得k=3,
即当k取3时,点A的纵坐标为3;
(3)解方程组
得
或
,
∴B点坐标为(3,-1),
∴当-1<x<0或x>3时,反比例函数y=-
值大于一次函数y=-x+2的值.
|
∴△=(-2)2-4(-k)≥0,解得k>-1,
∴k的取值范围为k>-1且k≠0;
(2)把y=3代入y=-x+2得-x+2=3,解得x=-1,
∴A点坐标为(-1,3),
把A(-1,3)代入y=-
| k |
| x |
即当k取3时,点A的纵坐标为3;
(3)解方程组
|
|
|
∴B点坐标为(3,-1),
∴当-1<x<0或x>3时,反比例函数y=-
| k |
| x |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.

练习册系列答案
相关题目
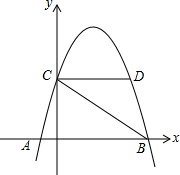 如图,抛物线y=-x2+3x+4与x轴交于A、B两点,与y轴交于点C,CD∥x轴交抛物线于点D,连接DB,在抛物线上是否存在一点P,使∠DBP=∠ABC?若存在,求出点P的坐标;若不存在,说明理由.
如图,抛物线y=-x2+3x+4与x轴交于A、B两点,与y轴交于点C,CD∥x轴交抛物线于点D,连接DB,在抛物线上是否存在一点P,使∠DBP=∠ABC?若存在,求出点P的坐标;若不存在,说明理由. 如图,?OABC的顶点坐标分别为O(0,0),A(6,0),C(3,4).求:
如图,?OABC的顶点坐标分别为O(0,0),A(6,0),C(3,4).求: 如图,在△ABC中,∠CAB=90°,AB=3,AC=4,AD是∠CAB的平分线,AD交BC于D,求BD的长.
如图,在△ABC中,∠CAB=90°,AB=3,AC=4,AD是∠CAB的平分线,AD交BC于D,求BD的长.