题目内容
【题目】解决下列两个问题:
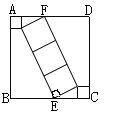
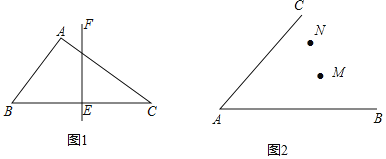
(1)如图1,在△ABC中,AB=4,AC=6,BC=7,EF垂直平分BC,P为直线EF上一动点,PA+PB的最小值为______,并在图中标出当PA+PB取最小值时点P的位置.
(2)如图2,点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)
【答案】(1)6,图形见解析;(2)见解析.
【解析】
(1)根据垂直平分线的性质得![]() ,因此
,因此![]() ,再根据三角形的三边关系得,
,再根据三角形的三边关系得,![]() ,故当点P在AC边上,
,故当点P在AC边上,![]() 取最小值AC,即
取最小值AC,即![]() 取最小值;
取最小值;
(2)画![]() 的角平分线和线段MN的垂直平分线,两条线相交于点P即为所求作的点.
的角平分线和线段MN的垂直平分线,两条线相交于点P即为所求作的点.
(1)根据垂直平分线的性质得![]() ,则
,则![]()
在![]() 中,根据三角形的三边关系得,
中,根据三角形的三边关系得,![]()
故当点P在AC边上,![]() 取最小值AC
取最小值AC
即当点P在AC边上,![]() 取得最小值,此时
取得最小值,此时![]()
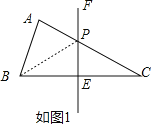
答:![]() 的最小值为6,此时点P的位置如图1所示.
的最小值为6,此时点P的位置如图1所示.
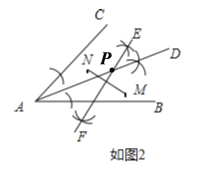
(2)由题意得,画![]() 的角平分线和线段MN的垂直平分线,两条线相交于点P即为所求作的点.如图2所示:
的角平分线和线段MN的垂直平分线,两条线相交于点P即为所求作的点.如图2所示:

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目