题目内容
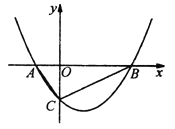
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其顶点在直线
,其顶点在直线![]() 上.
上.
(1)求![]() 的值;
的值;
(2)求![]() 两点的坐标;
两点的坐标;
(3)以![]() 为一组邻边作
为一组邻边作![]() ,则点
,则点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 是否在该抛物线上?
是否在该抛物线上?
请说明理由.
【答案】(1)
【解析】分析:(1)根据二次函数的顶点坐标的求法得出顶点坐标,再代入一次函数即可求出a的值;
(2)根据二次函数解析式求出与x轴的交点坐标即是A,B两点的坐标;
(3)根据平行四边形的性质得出D点的坐标,即可得出D′点的坐标,即可得出答案.
详解:(1)抛物线y=x2﹣x+a=(x2﹣2x)+a=(x﹣1)2﹣+a,
∴抛物线顶点坐标为:(1,﹣![]() +a)
+a)
∵抛物线y=x2﹣x+a其顶点在直线y=﹣2x上
则将顶点坐标代入y=﹣2x得
﹣![]() +a=﹣2,∴a=﹣
+a=﹣2,∴a=﹣![]() ;
;
(2)由(1)写出抛物线解析式为:y=x2﹣![]() x﹣
x﹣![]()
∵抛物线y=![]() x2﹣x﹣
x2﹣x﹣![]() 与x轴交于点A、B,
与x轴交于点A、B,
∴0=![]() x2﹣x﹣
x2﹣x﹣![]() ,整理得:x2﹣2x﹣3=0,
,整理得:x2﹣2x﹣3=0,
解得:x=﹣1或3,
∴A(﹣1,0),B(3,0);
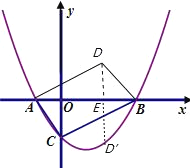
(3)作出平行四边形ACBD,作DE⊥AB,
∵二次函数解析式为:y=![]() x2﹣x﹣
x2﹣x﹣![]()
∴图象与y轴交点坐标为:(0,﹣![]() ),∴CO=
),∴CO=![]() ,DE=
,DE=![]() ,
,
∵∠CAO=∠DBE,∠DEB=∠AOC ∴△AOC≌△BDE
∴AO=BE=1, OE=OB-BE=2
∴D点的坐标为:(2,![]() ),
),
则点D关于x轴的对称点D′坐标为:(2,﹣![]() ),
),
代入解析式y=![]() x2﹣x﹣
x2﹣x﹣![]() ,左边=﹣
,左边=﹣![]() ,右边=
,右边=![]() ×4﹣2﹣
×4﹣2﹣![]() =﹣
=﹣![]() ,
,
∴D′点在函数图象上.

【题目】如图1是流花河的水文资料(单位:米),取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?如表是小明记录的今年雨季流花河一周内水位变化情况(上周末的水位达到警戒水位)
星期 水位 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.2 | +0.8 | -0.4 | +0.1 | +0.3 | -0.4 | -0.1 |
实际水位/米 | 33.6 |
注:正表示水位比前一天上升,负表示水位比前一天下降.

(1)本周星期______河流的水位最高,水位在警戒水位之______(上或下);星期______河流的水位最低,水位在警戒水位之______(上或下);
(2)与上周相比,本周末河流水位是______(上升了或下降了);
(3)完成上面的实际水位记录;
(4)以警戒水位为0点,用折线统计图(如图2)表示本周的水位情况.