题目内容
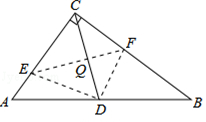
(如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).

(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为_________;
②当AC=3,BC=4时,AD的长为_________;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.

(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为_________;
②当AC=3,BC=4时,AD的长为_________;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
(1)①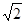 ;②
;②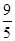 或
或 ;(2)△CEF与△ABC相似.理由详见解析.
;(2)△CEF与△ABC相似.理由详见解析.
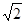 ;②
;②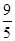 或
或 ;(2)△CEF与△ABC相似.理由详见解析.
;(2)△CEF与△ABC相似.理由详见解析.试题分析:(1)①如图1,有△CEF与△ABC相似,可得∠CEF=∠A=45°,由题意知△CEF≌△DEF,所以CE=DE,∠DEF=∠CEF=45°,所以∠DEC=90°,即∠AED=90°,又∠A=45°,所以△AED是等腰直角三角形,所以AE=DE,所以AE=CE=1,根据勾股定理可求得AD=
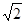 .②分两种情况:一、当△CEF∽△CAB时,如图2,则有∠CEF=∠CAB,所以EF∥AB,根据题意,点C与点D关于直线EF对称,所以CD⊥EF,所以CD⊥AB,由三角形的面积公式可求得CD=2.4,在△ACD中,由勾股定理可得AD=
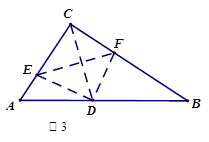
.②分两种情况:一、当△CEF∽△CAB时,如图2,则有∠CEF=∠CAB,所以EF∥AB,根据题意,点C与点D关于直线EF对称,所以CD⊥EF,所以CD⊥AB,由三角形的面积公式可求得CD=2.4,在△ACD中,由勾股定理可得AD=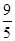 ;二、当△CFE∽△CAB时,如图3,此时有∠A=∠CFE, ∠B=∠CEF,又∠A+∠B=90°,所以∠A+∠CEF="90°," ∠B+∠CFE=90°,前面已证EF⊥CD,所以∠DCE+∠CEF=90°,∠DCF+∠CFE=90°,所以∠A=∠ACD, ∠B=∠BCD,所以AD=CD=BD=2.5;(2)利用折叠前后对应的部分关于折叠线对称,以及直角三角形斜边上的中线等于斜边的一半,即可求得∠A=∠CFE, ∠B=∠CEF,所以得证.
;二、当△CFE∽△CAB时,如图3,此时有∠A=∠CFE, ∠B=∠CEF,又∠A+∠B=90°,所以∠A+∠CEF="90°," ∠B+∠CFE=90°,前面已证EF⊥CD,所以∠DCE+∠CEF=90°,∠DCF+∠CFE=90°,所以∠A=∠ACD, ∠B=∠BCD,所以AD=CD=BD=2.5;(2)利用折叠前后对应的部分关于折叠线对称,以及直角三角形斜边上的中线等于斜边的一半,即可求得∠A=∠CFE, ∠B=∠CEF,所以得证.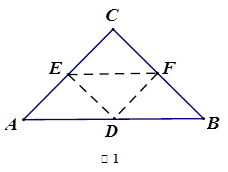

试题解析:(1)①
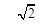 ;②
;②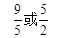 ;
;(2)△CEF与△ABC相似.理由如下:
如图,连接CD,与EF交于点Q.
∵CD是Rt△ABC的中线,
∴CD=DB=
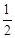 AB,∴∠DCB=∠B.
AB,∴∠DCB=∠B.由折叠性质可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°,
∵∠B+∠A=90°,
∴∠CFE=∠A,
又∵∠ECF=∠BCA,
∴△CEF∽△CBA.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
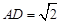 ,
,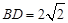 ,求AB的值.
,求AB的值.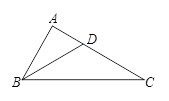


 的值 .
的值 .


 =DM·EN
=DM·EN
 ,则
,则 .
.