题目内容
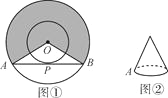
【题目】如图①,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1.
(1)用阴影部分的扇形围成一个圆锥(OA与OB重合),求该圆锥的底面半径.
(2)用余下部分再围成一个圆锥(如图②所示),若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,求小虫爬行的最短路线的长.
【答案】(1)圆锥的底面半径为![]() ;(2)小虫爬行的最短路线为
;(2)小虫爬行的最短路线为![]() .
.
【解析】
(1)利用30°角的性质可求得∠A的度数,进而求出∠AOB的度数,可求优弧AB的长度,除以2π即为圆锥的底面半径;
(2)由题意知,小虫爬行的最短路线是弦AB的长,利用垂径定理和勾股定理即可求得弦AB的长;
(1)连接OP,

则OP⊥AB,
∵OA=2,OP=1,
∴∠A=30°,
∴∠AOB=180°-30°-30°=120°,
∴优弧AB的长为:![]()
∴圆锥的底面半径为:![]() =
=![]()
(2)由勾股定理得,AP=![]() ,
,
∵OP⊥AB,
∴AB=2AP=![]() .
.
∴小虫爬行的最短路线为![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目