��Ŀ����
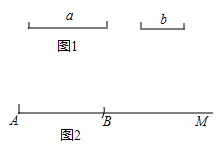
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊa����B��ʾ����Ϊb��������![]() ��
��
![]() д��a��b��AB�ľ��룺
д��a��b��AB�ľ��룺
![]() ______
______ ![]() ______
______ ![]() ______
______
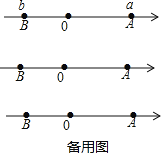
![]() ������P�ӵ�A��������ÿ��6����λ�������������������˶�������Q�ӵ�B��������ÿ��4����λ�������������˶���
������P�ӵ�A��������ÿ��6����λ�������������������˶�������Q�ӵ�B��������ÿ��4����λ�������������˶���
![]() ��P��Qͬʱ�������ʵ�P�˶��������ϵ�Q��
��P��Qͬʱ�������ʵ�P�˶��������ϵ�Q��
![]() ��MΪAP���е㣬NΪPB���е㣬��P���˶������У��߶�MN�Ƿ����仯�����仯����˵�����ɣ������䣬������߶�MN�ij���
��MΪAP���е㣬NΪPB���е㣬��P���˶������У��߶�MN�Ƿ����仯�����仯����˵�����ɣ������䣬������߶�MN�ij���
���𰸡���1��6�� ![]() ��10����2������P�˶�5��ʱ�ϵ�Q���߶�MN�������仯
��10����2������P�˶�5��ʱ�ϵ�Q���߶�MN�������仯
�����������������(1)���ݷǸ��������ʿɵ�a-6=0,b+4=0,�����a��b��ֵ,Ȼ��ɼ����AB�ij���;
(2)�����P�˶�t��ʱ�ϵ�Q,��������ɵõ�����ϵ:��P�˶���·��-��Q�˶���·��![]() ,���ݵ�����ϵ�г�����,�ٽ⼴��;
,���ݵ�����ϵ�г�����,�ٽ⼴��;
�ڴ���Ҫ���������:��P���߶�AB֮��ʱ;��P���߶�AB���ӳ�����ʱ,�ֱ�ͼ��,�����߶�֮��Ĺ�ϵ���м��㼴��.
�⣺ ![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��
�ʴ�Ϊ��6�� ![]() ��10��
��10��
![]() ���P�˶�t��ʱ�ϵ�Q����
���P�˶�t��ʱ�ϵ�Q����
![]() ��
��
![]() ��
��
������P�˶�5��ʱ�ϵ�Q��
![]() ���߶�MN�������仯�����ɣ�
���߶�MN�������仯�����ɣ�
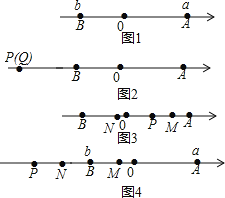
��P���߶�AB֮��ʱ��
![]() ��
��
= ![]()
![]() ��
��
![]() ��
��
��P���߶�AB���ӳ�����ʱ��
![]() ��
��
��MN�ij��������仯��

����Ŀ������ı��������ͬѧһѧ����ѧ�ɼ��ļ�¼�����ݱ����ṩ����Ϣ�ش����������
������� | ƽʱ | ���п��� | ��ĩ���� | |||
��һ��Ԫ | �ڶ���Ԫ | ������Ԫ | ���ĵ�Ԫ | |||
�ɼ� | 88 | 86 | 90 | 92 | 90 | 96 |

��1�����ͬѧ6�γɼ������� ��
��2�����ͬѧ6�γɼ�����λ���� ��
��3�����ͬѧƽʱ�ɼ���ƽ������ ��
��4���������ͼ��Ȩ�ظ���մ�֣���Ӧ�õö��ٷ֣�������100�֣�д��������̣�