题目内容
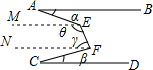
如图，AB∥CD，∠A=α,∠C=β,∠AEF=θ，∠EFC=γ，用含α、β、γ的式子表示θ，则θ=（ ）
| A．α+γ﹣β | B．β+γ﹣α | C．180°+γ﹣α﹣β | D．180°+α+β﹣γ |
D
过点E作EM∥AB，过点F作FN∥CD，由平行线的传递性得，AB∥EM∥NF∥CD，
∵EM∥AB，∴∠α=∠AEM，∵FN∥CD，∴∠β=∠CFN，
∵EM∥FN，∴∠MEF+∠EFN=180°，
又∵∠θ=∠AEM+∠MEF=∠α+180°-（∠γ-∠β）=180°+∠α+∠β-∠γ．故选D．
∵EM∥AB，∴∠α=∠AEM，∵FN∥CD，∴∠β=∠CFN，
∵EM∥FN，∴∠MEF+∠EFN=180°，
又∵∠θ=∠AEM+∠MEF=∠α+180°-（∠γ-∠β）=180°+∠α+∠β-∠γ．故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
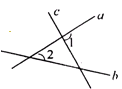
被直线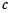
所截，给出下列条件：①∠1=∠2 , ②∠2=∠3,③∠3=∠4 , ④∠4=180°-∠1. 其中能判断
∥
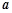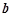的条件是 ( 填序号)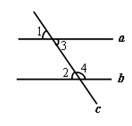
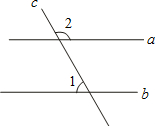
、b分别相交于M、N.若