题目内容
已知二次函数图象的顶点坐标为M（3，﹣2），且与y轴交于N（0，
）。
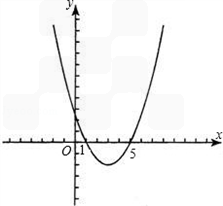
（1）求该二次函数的解析式，并用列表、描点画出它的图象；
（2）若该图象与x轴交于A、B两点，在对称轴右侧的图象上存在点C，使得△ABC的面积等于12，求出C点的坐标．
）。（1）求该二次函数的解析式，并用列表、描点画出它的图象；
（2）若该图象与x轴交于A、B两点，在对称轴右侧的图象上存在点C，使得△ABC的面积等于12，求出C点的坐标．
解：（1）由于二次函数图象的顶点是（3，﹣2），
设所求的二次函数解析式是y=a（x﹣3）2﹣2，
由于所求图象过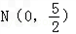
，
可得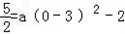
，
解得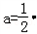
所以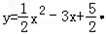
列表：
（2）当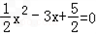
时，x1=1，x2=5，
∴点A（1，0），点B（5，0），则AB=4，
∵△ABC的面积为12，
∴
，
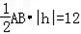∴|h|=6，
∴抛物线顶点是（3，﹣2），
h1=6，h2=﹣6（舍去），
∵
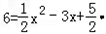
解出，x1=7，x2=﹣1，
由于抛物线对称轴是x=3，所以x2=﹣1（舍去），有点C（7，6）。
设所求的二次函数解析式是y=a（x﹣3）2﹣2，
由于所求图象过
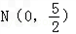，可得
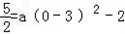，解得
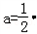
所以
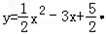
列表：
（2）当
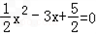时，x1=1，x2=5，∴点A（1，0），点B（5，0），则AB=4，
∵△ABC的面积为12，
∴
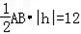，∴|h|=6，
∴抛物线顶点是（3，﹣2），
h1=6，h2=﹣6（舍去），
∵
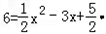
解出，x1=7，x2=﹣1，
由于抛物线对称轴是x=3，所以x2=﹣1（舍去），有点C（7，6）。
练习册系列答案
相关题目
OC相似？若存在，请求出P点的坐标；若不存在，请说明理由．
已知二次函数图象的顶点是（-1，2），且过点
已知二次函数图象的顶点坐标为M（3，-2），且与y轴交于N（0，
点（A在B的左侧），且A点坐标为（-4，4）．平行于x轴的直线l过（0，-1）点．
于点Q，设线段PQ的长为l，点P的横坐标为x．