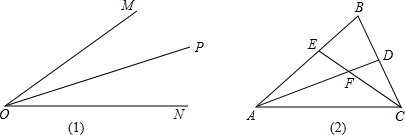题目内容
请同学们试一试：
（1）如图（1），OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．
（2）猜想一下：在一个三角形中，两个内角平分线相交而成的一个钝角的度数与第三个内角的度数之间有什么关系？（写出结论，并证明）（温馨提醒：要画图、写已知、求证．） 下面的证明如果要用此题结论，则可以直接用．
（3）如图（2）在△ABC中，∠B=60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F，请你判别并写出FE与FD之间的数量关系；并证明你的结论．
（1）如图（1），OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．
（2）猜想一下：在一个三角形中，两个内角平分线相交而成的一个钝角的度数与第三个内角的度数之间有什么关系？（写出结论，并证明）（温馨提醒：要画图、写已知、求证．） 下面的证明如果要用此题结论，则可以直接用．
（3）如图（2）在△ABC中，∠B=60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F，请你判别并写出FE与FD之间的数量关系；并证明你的结论．
分析：（1）在OM、ON上截取相同长度的线段，在OP上任取一点A，构造全等三角形即可；
（2）由在△ABC中，OB、OC是∠ABC、∠ACB的角平分线，根据三角形的内角和定理即可求得∠OBC+∠OCB的值，然后在△OBC中，再利用三角形的内角和定理，即可求得答案；
（3）通过证明△EAF≌△HAF（SAS），△FCH≌△FCD（ASA），根据全等三角形的性质即可得出结论．
（2）由在△ABC中，OB、OC是∠ABC、∠ACB的角平分线，根据三角形的内角和定理即可求得∠OBC+∠OCB的值，然后在△OBC中，再利用三角形的内角和定理，即可求得答案；
（3）通过证明△EAF≌△HAF（SAS），△FCH≌△FCD（ASA），根据全等三角形的性质即可得出结论．
解答：解：（1）作法：①以O为圆心，任意长为半径作弧，分别交射线ON，OM于C，B两点；
②在射线OP上任取一点A（O点除外）；
③连接AB，AC．
则所得△AOB≌△AOC．
作图如下：
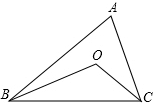（2）已知：如图，在△ABC中，OB、OC分别是∠ABC、∠ACB的角平分线；求证：∠BOC=90°+
∠A．
证明：∵在△ABC中，OB、OC是∠ABC、∠ACB的角平分线；
∴∠OBC=
∠ABC，∠OCB=
∠ACB，
∵∠ABC+∠ACB=180°-∠A，
∴∠OBC+∠OCB=
（∠ABC+∠ACB）=
（180°-∠A）=90°-
∠A，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-
∠A）=90°+
∠A；
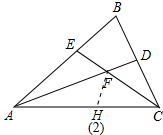（3）FE与FD之间的数量关系是EF=FD．理由如下：
在AC上截取AH=AE．
∵AD是∠EAC的平分线，
∴∠EAF=∠HAF．
在△EAF与△HAF中，
∵
，
∴△EAF≌△HAF（SAS），
∴∠EFA=∠AFH，
∵∠B=60°．
∴由（2）得∠AFC=90°+
∠B=120°，
∴∠AFE=180°-∠AFC=60°=∠DFC．
∵∠EFA=∠AFH=60°，
∴∠HFC=180°-∠EFA-∠AFH=60°，
∴∠DFC=∠HFC．
∵CE是∠ACD的平分线，
∴∠FCH=∠FCD．
∵在△FCH与△FCD中，
，
∴△FCH≌△FCD（ASA），
∴FD=FH．
∵△EAF≌△HAF，
∴FE=FH，
∴EF=FD．
②在射线OP上任取一点A（O点除外）；
③连接AB，AC．
则所得△AOB≌△AOC．
作图如下：
（2）已知：如图，在△ABC中，OB、OC分别是∠ABC、∠ACB的角平分线；求证：∠BOC=90°+| 1 |
| 2 |
证明：∵在△ABC中，OB、OC是∠ABC、∠ACB的角平分线；
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC+∠ACB=180°-∠A，
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-
| 1 |
| 2 |
| 1 |
| 2 |
（3）FE与FD之间的数量关系是EF=FD．理由如下：在AC上截取AH=AE．
∵AD是∠EAC的平分线，
∴∠EAF=∠HAF．
在△EAF与△HAF中，
∵
|
∴△EAF≌△HAF（SAS），
∴∠EFA=∠AFH，
∵∠B=60°．
∴由（2）得∠AFC=90°+
| 1 |
| 2 |
∴∠AFE=180°-∠AFC=60°=∠DFC．
∵∠EFA=∠AFH=60°，
∴∠HFC=180°-∠EFA-∠AFH=60°，
∴∠DFC=∠HFC．
∵CE是∠ACD的平分线，
∴∠FCH=∠FCD．
∵在△FCH与△FCD中，
|
∴△FCH≌△FCD（ASA），
∴FD=FH．
∵△EAF≌△HAF，
∴FE=FH，
∴EF=FD．
点评：本题考查的是熟练掌握尺规作图的技巧和三角形全等的判定定理．同时考查了角平分线的性质，全等三角形的判定与性质以及直角三角形的性质．此题难度较大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
练习册系列答案
相关题目
