Question

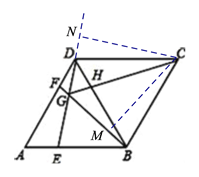
【题目】如图，在菱形ABCD中，AB=BD．点E、F分别在AB、AD上，且AE=DF．连接BF与DE相交于点G，连接CG与BD相交于点H．下列结论：①△AED≌△DFB； ②S四边形BCDG=CG2；③DE=CG；④若AF=2DF，则BG=6GF．其中正确的结论_____________．

Answer 1

【答案】1 2 4

【解析】分析：（1）由已知条件易得∠A=∠BDF=60°，结合BD=AB=AD，AE=DF，即可证得△AED≌△DFB，从而说明结论①正确；（2）由已知条件可证点B、C、D、G四点共圆，从而可得∠CDN=∠CBM，如图，过点C作CM⊥BF于点M，过点C作CN⊥ED于点N，结合CB=CD即可证得△CBM≌△CDN，由此可得S四边形BCDG=S四边形CMGN=2S△CGN，在Rt△CGN中，由∠CGN=∠DBC=60°，∠CNG=90°可得GN=CG，CN=CG，由此即可求得S△CGN=CG2，从而可得结论②是正确的；（3）由已知易得△ADE中，∠AED>∠A=60°，从而可得AD>DE；在△DCG中，∠CDG>∠CGD=60°，从而可得CG>DC；结合AD=CD即可得到CG>DE，从而说明结论③错误；（4）过点F作FK∥AB交DE于点K，由此可得△DFK∽△DAE，△GFK∽△GBE，结合AF=2DF和相似三角形的性质即可证得结论④成立.

详解：

（1）∵四边形ABCD是菱形，BD=AB，

∴AB=BD=BC=DC=DA，

∴△ABD和△CBD都是等边三角形，

∴∠A=∠BDF=60°，

又∵AE=DF，

∴△AED≌△DFB，即结论①正确；

（2）∵△AED≌△DFB，△ABD和△DBC是等边三角形，

∴∠ADE=∠DBF，∠DBC=∠CDB=∠BDA=60°，

∴∠GBC+∠CDG=∠DBF+∠DBC+∠CDB+∠GDB=∠DBC+∠CDB+∠GDB+∠ADE=∠DBC+∠CDB+∠BDA=180°，

∴点B、C、D、G四点共圆，

∴∠CDN=∠CBM，

如下图，过点C作CM⊥BF于点M，过点C作CN⊥ED于点N，

∴∠CDN=∠CBM=90°，

又∵CB=CD，

∴△CBM≌△CDN，

∴S四边形BCDG=S四边形CMGN=2S△CGN，

∵在Rt△CGN中，∠CGN=∠DBC=60°，∠CNG=90°

∴GN=CG，CN=CG，

∴S△CGN=CG2，

∴S四边形BCDG=2S△CGN，=CG2，即结论②是正确的；

（3）∵在△ABD是等边三角形，

∴∠A=60°，∠AED>∠ABD=60°，

∴∠AED>∠A，

∴DE<AD，

同理，在△DGC中：∠GDC>∠DGC，

∴CG>CD，

∵AD=CD，

∴DE<CG，即结论③错误；

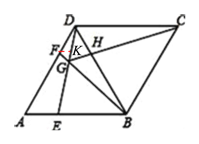
（4）如下图，过点F作FK∥AB交DE于点K，

∴△DFK∽△DAE，△GFK∽△GBE，

∴，，

∵AF=2DF，

∴，

∵AB=AD，AE=DF，AF=2DF，

∴BE=2AE，

∴，

∴BG=6FG，即结论④成立.

综上所述，本题中正确的结论是：

故答案为：①②④.