题目内容
(本小题14分)如图,已知在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒。

1.(1)(4分)如果P、Q分别从A、B两点同时出发,那么几秒后,△PBQ的面积等于△ABC的面积的![]() ?
?
2.(2)(5分)若P、Q分别从A、B两点出发,那么几秒后,PQ的长度等于6cm?
3.(3)(5分)P、Q在移动的过程中,是否存在某一时刻t,使得PQ∥AC,若存在求出t的值,若不存在请说明理由。
1.(1)∵P、Q移动t秒时AP=t,BQ=2t
则PB=AB-AP=6-t
∴S△PBQ=![]()
∵S△ABC=![]() =
=![]()
当S△PBQ=![]() S△ABC时,则t(6-t)=
S△ABC时,则t(6-t)=![]()
t2-6t+8=0
t1=2, t2=4
∴当t=2或4时,△PBQ的面积等于△ABC的面积的![]() 。
。
2.
3.
解析:略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
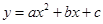 经过原点
经过原点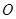 ,与
,与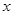 轴交于另一点
轴交于另一点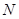 ,直线
,直线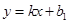 与两坐标轴分别交于
与两坐标轴分别交于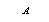 、
、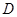 两点,与抛物线交于
两点,与抛物线交于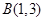 、
、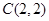 两点.
两点.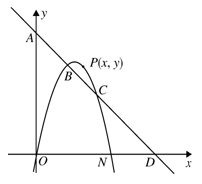
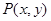 ,
,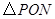 的面积最大值;
的面积最大值;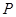 保持(2)中的运动路线,问是否存在点
保持(2)中的运动路线,问是否存在点 的面积等于
的面积等于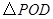 面积的
面积的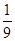 ?若存在,请求出点
?若存在,请求出点 P
P 从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒?
从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒?
 ?
? P
P 从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒?
从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒?
 ?
?
 ?
?