题目内容
如图，在正方形纸板上剪下一个扇形和圆，围成一个圆锥模型，设围成的圆锥底面半径为r，母线长为R，正方形的边长为a，则用r表示a为（ ）
A．a=
B．a=
C．a=
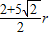
D．a=（1+
）
【答案】分析：利用底面周长=展开图的弧长求出半径比，再根据过小圆的圆心作垂线，垂直于正方形的边，就构成等腰直角三角形，从图中关系可知，直角三角形的斜边是r+R，直角边a-r，根据勾股定理计算．
解答：解：利用底面周长=展开图的弧长可得；
2πr=
，
得出R=4r，
利用勾股定理解得a=
．
故选C．
点评：本题的关键是利用底面周长=展开图的弧长求得r与R的关系，然后由勾股定理求得a与r之间的关系．
解答：解：利用底面周长=展开图的弧长可得；
2πr=
，得出R=4r，
利用勾股定理解得a=
．故选C．
点评：本题的关键是利用底面周长=展开图的弧长求得r与R的关系，然后由勾股定理求得a与r之间的关系．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
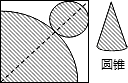如图，在正方形纸板上剪下一个扇形和圆，围成一个圆锥模型，设围成的圆锥底面半径为r，母线长为R，正方形的边长为a，则用r表示a为（ ）A、a=
| ||||
B、a=
| ||||
C、a=
| ||||
D、a=（1+
|
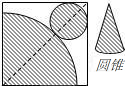如图，在正方形纸板上剪下一个扇形和圆，刚好能围成一个圆锥模型，设围成的圆锥底面半径为r，母线长为R，则r与R之间的关系为（ ）| A、R=2r | B、4R=9r | C、R=3r | D、R=4r |
）
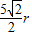