题目内容
如图，在正方形纸板上剪下一个扇形和圆，刚好能围成一个圆锥模型，设围成的圆锥底面半径为r，母线长为R，则r与R之间的关系为（ ）
A．R=2r
B．4R=9r
C．R=3r
D．R=4r
【答案】分析：求得侧面展开图的弧长，以及圆锥的底面周长，让它们相等即可求得r与R之间的关系．
解答：解：由题意得：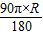
=2πr，
解得：R=4r，
故选D．
点评：用到的知识点为：圆锥的侧面展开图的弧长等于圆锥的底面周长．
解答：解：由题意得：
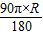=2πr，解得：R=4r，
故选D．
点评：用到的知识点为：圆锥的侧面展开图的弧长等于圆锥的底面周长．
练习册系列答案
相关题目
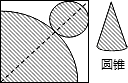如图，在正方形纸板上剪下一个扇形和圆，围成一个圆锥模型，设围成的圆锥底面半径为r，母线长为R，正方形的边长为a，则用r表示a为（ ）A、a=
| ||||
B、a=
| ||||
C、a=
| ||||
D、a=（1+
|
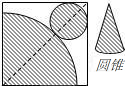如图，在正方形纸板上剪下一个扇形和圆，刚好能围成一个圆锥模型，设围成的圆锥底面半径为r，母线长为R，则r与R之间的关系为（ ）| A、R=2r | B、4R=9r | C、R=3r | D、R=4r |
）
）
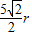
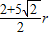