题目内容
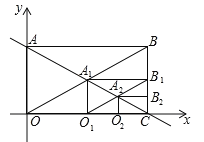
【题目】如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
![]()
A.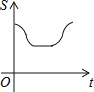 B.
B.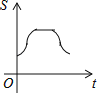
C.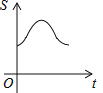 D.
D.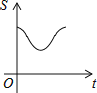
【答案】A
【解析】
设三角形运动速度为1,根据勾股定理可求出等腰直角三角形的斜边长为![]() ,分0≤t≤
,分0≤t≤![]() 时,
时,![]() <t≤
<t≤![]() 时,
时,![]() <t≤2时,2<t≤2+
<t≤2时,2<t≤2+![]() 时,2+
时,2+![]() <t≤2+
<t≤2+![]() 时五种情况,可知等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大,分别求出函数关系式,即可得出答案.
时五种情况,可知等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大,分别求出函数关系式,即可得出答案.
∵等腰直角三角形的直角边长为1,
∴等腰直角三角形的斜边长为![]() =
=![]() ,
,
当0≤t≤![]() 时,s=
时,s=![]() ×1×1+2×2﹣
×1×1+2×2﹣![]() =
=![]() ﹣
﹣![]() t2;
t2;
当![]() <t≤
<t≤![]() 时,s=22-
时,s=22-![]() +2×
+2×![]() (
(![]() -t)2=t2﹣2
-t)2=t2﹣2![]() t+
t+![]() ;
;
当![]() <t≤2时,s=
<t≤2时,s=![]() ×1×1=
×1×1=![]() ;
;
当2<t≤2+![]() 时,s=22-2×
时,s=22-2×![]() (t-2)2=t2﹣4t+
(t-2)2=t2﹣4t+![]() ;
;
当2+![]() <t≤2+
<t≤2+![]() 时,s=22+
时,s=22+![]() -2×
-2×![]() (
(![]() ﹣t+2)2=
﹣t+2)2=![]() ﹣(
﹣(![]() ﹣t+2)2,
﹣t+2)2,
∴等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大,且变小、变大时的图象为抛物线,不变时的图象为直线,
∴A符合要求,
故选:A.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目