题目内容
(2004•河南)已知a>2,b>2,试判断关于x的方程x2-(a+b)x+ab=0与x2-abx+(a+b)=0有没有公共根.请说明理由.
【答案】分析:两个方程有公共根,就是两方程组成的方程组有解.
解答:解:不妨设关于x的方程x2-(a+b)x+ab=0与x2-abx+(a+b)=0有公共根,设为x,
则有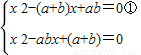 ,
,
整理可得(x+1)(a+b-ab)=0.
∵a>2,b>2,
∴a+b≠ab,
∴x=-1;
把x=-1代入①得1+a+b+ab=0,这是不可能的.
所以关于x的两个方程没有公共根.
点评:本题考查了一元二次方程的根的判断,正确对方程组中的两个方程进行整理是关键.
解答:解:不妨设关于x的方程x2-(a+b)x+ab=0与x2-abx+(a+b)=0有公共根,设为x,
则有
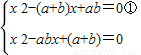 ,
,整理可得(x+1)(a+b-ab)=0.
∵a>2,b>2,
∴a+b≠ab,
∴x=-1;
把x=-1代入①得1+a+b+ab=0,这是不可能的.
所以关于x的两个方程没有公共根.
点评:本题考查了一元二次方程的根的判断,正确对方程组中的两个方程进行整理是关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 与
与 有没有公共根,请说明理由.
有没有公共根,请说明理由.
