题目内容
【题目】如图，已知AD∥BC，点E为CD上一点，AE，BE分别平分∠DAB，∠CBA．
（1）求证：AE⊥BE；
（2）求证：DE=CE；
（3）若AE=4，BE=6，求四边形ABCD的面积．
【答案】（1）详见解析；（2）详见解析；（3）24
【解析】
（1）根据平行线的性质及角平分线的定义进行角度的计算即可得解；
（2）通过证明
及
，再由其性质进行证明即可得解；
（3）通过
进行求解即可.
（1）证明：∵
∴
∵AE，BE分别平分∠DAB，∠CBA
∴
，
∴
∴
，即AE⊥BE；
（2）证明：如下图，延长AE交BC的延长线于点F．
∵
∴
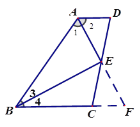
∵∠4=∠3，BE=BE
∴
∴AE=EF
∵AD∥BC
∴∠2=∠F，∠D=∠DCF
∴
∴DE=CE；
（3）证明：由（2）知，
∴
∴
由（2）知，EF=AE=4，即AF=8
∵BE=6
∴
.
练习册系列答案
名校课堂系列答案
相关题目
