题目内容
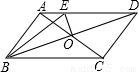
(2007•日照)如图,AC⊥BC于点C,BC=a,CA=b,AB=c,⊙O与直线AB、BC、CA都相切,则⊙O的半径等于 .
【答案】分析:设AC、BA、BC与⊙O的切点分别为D、F、E;由勾股定理可得:BF=BE,AF=AD,CD=CE;可用DC分别表示出BE、BF的长,根据BF=BE,得出CD的表达式;连接OD、OE;易证得四边形ODCE是正方形,即OE=OD=CD,由此可求出⊙O的半径.
解答:解:设AC、BA、BC与⊙O的切点分别为D、F、E;连接OD、OE;
∵AC、BE是⊙O的切线,
∴∠ODC=∠OEC=∠DCE=90°;
∴四边形ODCE是矩形;
∵OD=OE,
∴矩形ODCE是正方形;
即OE=OD=CD;
设CD=CE=x,则AD=AF=b-x;
连接OB,OF,
由勾股定理得:BF2=OB2-OF2,BE2=OB2-OE2,
∵OB=OB,OF=OE,
∴BF=BE,
则BA+AF=BC+CE,c+b-x=a+x,即x= ;
;
故⊙O的半径为 .
.
点评:此题主要考查了正方形性质和判定和勾股定理的应用.
解答:解:设AC、BA、BC与⊙O的切点分别为D、F、E;连接OD、OE;

∵AC、BE是⊙O的切线,
∴∠ODC=∠OEC=∠DCE=90°;
∴四边形ODCE是矩形;
∵OD=OE,
∴矩形ODCE是正方形;
即OE=OD=CD;
设CD=CE=x,则AD=AF=b-x;
连接OB,OF,
由勾股定理得:BF2=OB2-OF2,BE2=OB2-OE2,
∵OB=OB,OF=OE,
∴BF=BE,
则BA+AF=BC+CE,c+b-x=a+x,即x=
 ;
;故⊙O的半径为
 .
.点评:此题主要考查了正方形性质和判定和勾股定理的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目