题目内容
把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点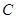 顺时针旋转
顺时针旋转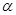 角,
旋转后的矩形记为矩形
角,
旋转后的矩形记为矩形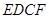 .在旋转过程中,
.在旋转过程中,
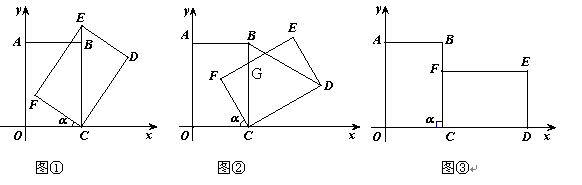
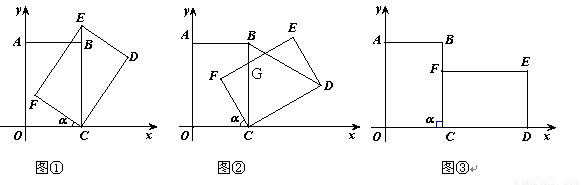
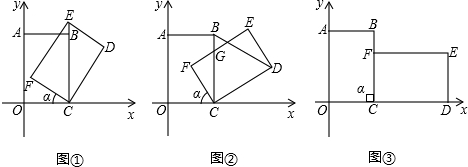
1.(1)如图①,当点E在射线CB上时,E点坐标为 ;
2.(2)当 是等边三角形时,旋转角
是等边三角形时,旋转角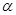 的度数是
(
的度数是
(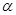 为锐角时);
为锐角时);
3.(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标.
4.(4) 如图③,当旋转角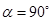 时,请判断矩形
时,请判断矩形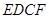 的对称中心H是否在以C为顶点,且经过点A的抛物线上.
的对称中心H是否在以C为顶点,且经过点A的抛物线上.
【答案】
1.(1)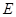 (4,
(4, )
)
2.(2)
3.(3)设 ,则
,则 ,
, ,
,
在Rt△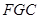 中,∵
中,∵ ,∴
,∴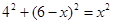 ,
,
解得  ,即
,即 .
.
∴ (4,
(4, ). …………………………………………………………4分
). …………………………………………………………4分
4.(4)设以点 为顶点的抛物线的解析式为
为顶点的抛物线的解析式为 .
.
把 (0,6)代入得,
(0,6)代入得, .
.
解得,  .
.
∴此抛物线的解析式为 .……………………………………6分
.……………………………………6分
∵矩形 的对称中心为对角线
的对称中心为对角线 、
、 的交点
的交点 ,
,
∴由题意可知 的坐标为(7,2).
的坐标为(7,2).
当 时,
时, ,
,
∴点 不在此抛物线上.
不在此抛物线上.
【解析】略

练习册系列答案
相关题目


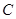 顺时针旋转
顺时针旋转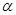 角, 旋转后的矩形记为矩形
角, 旋转后的矩形记为矩形 .在旋转过程中,
.在旋转过程中, 是等边三角形时,旋转角
是等边三角形时,旋转角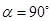 时,请判断矩形
时,请判断矩形 A的抛物线上.
A的抛物线上.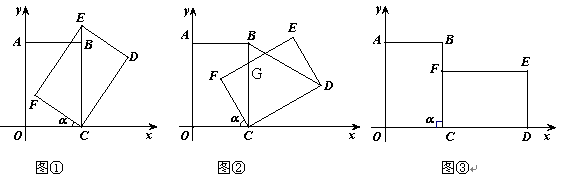
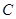 顺时针旋转
顺时针旋转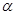 角, 旋转后的矩形记为矩形
角, 旋转后的矩形记为矩形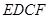 .在旋转过程中,
.在旋转过程中, 是等边三角形时,旋转角
是等边三角形时,旋转角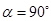 时,请判断矩形
时,请判断矩形 A的抛物线上.
A的抛物线上.