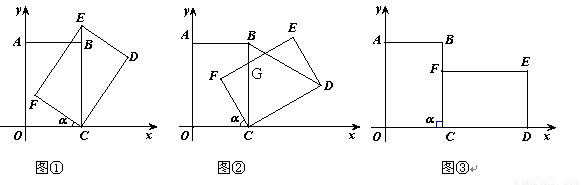
题目内容
把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,(1)如图①,当点E在射线CB上时,E点坐标为
(2)当△CBD是等边三角形时,旋转角a的度数是
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
分析:(1)依题意得点E在射线CB上,横坐标为4,纵坐标根据勾股定理可得点E.
(2)已知∠BCD=60°,∠BCF=30°,然后可得∠α=60°.
(3)设CG=x,则EG=x,FG=6-x,根据勾股定理求出CG的值.
(4)设以C为顶点的抛物线的解析式为y=a(x-4)2,把点A的坐标代入求出a值.当x=7时代入函数解析式可得解.
(2)已知∠BCD=60°,∠BCF=30°,然后可得∠α=60°.
(3)设CG=x,则EG=x,FG=6-x,根据勾股定理求出CG的值.
(4)设以C为顶点的抛物线的解析式为y=a(x-4)2,把点A的坐标代入求出a值.当x=7时代入函数解析式可得解.
解答:解.(1)E(4,2
)(l分)
(2)60°(2分)
(3)设CG=x,则EG=x,FG=6-x,
在Rt△FGC中,∵CF2+FG2=CG2,
∴42+(6-x)2=x2
解得x=
,
即CG=
∴G(4,
)(4分)
(4)设以C为顶点的抛物线的解析式为y=a(x-4)2,
把A(0,6)代入,得6=a(0-4)2.
解得a=
.
∴抛物线的解析式为y=
(x-4)2(6分)
∵矩形EDCF的对称中心H即为对角线FD、CE的交点,
∴H(7,2).
当x=7时,y=
(7-4)2=
≠2
∴点H不在此抛物线上.(7分)
| 13 |
(2)60°(2分)
(3)设CG=x,则EG=x,FG=6-x,
在Rt△FGC中,∵CF2+FG2=CG2,
∴42+(6-x)2=x2
解得x=
| 13 |
| 3 |
即CG=
| 13 |
| 3 |
∴G(4,
| 13 |
| 3 |
(4)设以C为顶点的抛物线的解析式为y=a(x-4)2,
把A(0,6)代入,得6=a(0-4)2.
解得a=
| 3 |
| 8 |
∴抛物线的解析式为y=
| 3 |
| 8 |
∵矩形EDCF的对称中心H即为对角线FD、CE的交点,
∴H(7,2).
当x=7时,y=
| 3 |
| 8 |
| 27 |
| 8 |
∴点H不在此抛物线上.(7分)
点评:本题考查的是二次函数的综合运用以及利用待定系数法求出函数解析式,难度较大.

练习册系列答案
相关题目

 顺时针旋转
顺时针旋转 角, 旋转后的矩形记为矩形
角, 旋转后的矩形记为矩形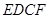 .在旋转过程中,
.在旋转过程中, 是等边三角形时,旋转角
是等边三角形时,旋转角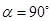 时,请判断矩形
时,请判断矩形 A的抛物线上.
A的抛物线上.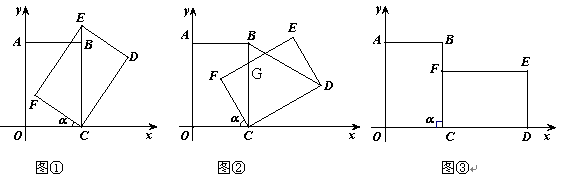
 顺时针旋转
顺时针旋转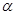 角, 旋转后的矩形记为矩形
角, 旋转后的矩形记为矩形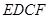 .在旋转过程中,
.在旋转过程中, 是等边三角形时,旋转角
是等边三角形时,旋转角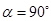 时,请判断矩形
时,请判断矩形 A的抛物线上.
A的抛物线上.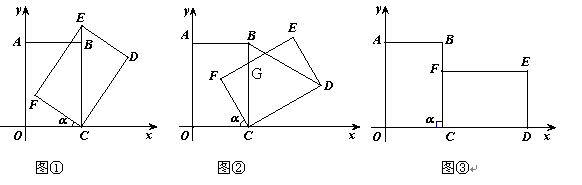
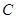 顺时针旋转
顺时针旋转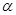 角,
旋转后的矩形记为矩形
角,
旋转后的矩形记为矩形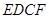 .在旋转过程中,
.在旋转过程中, 是等边三角形时,旋转角
是等边三角形时,旋转角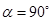 时,请判断矩形
时,请判断矩形