Question

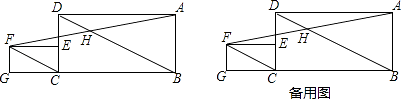
【题目】如图，AB是⊙O的一条弦，C是⊙O上一动点且∠ACB=45°，E、F分别是AC、BC的中点，直线EF与⊙O交于点G、H．若⊙O的半径为2，则GE+FH的最大值为 ．

Answer 1

【答案】4﹣ ．
【解析】连接OA，OB，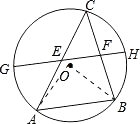

∵∠ACB=45°，∴∠AOB=90°．∵OA=OB，∴△AOB是等腰直角三角形，

∴AB=2 ，当GH为⊙O的直径时，GE+FH有最大值．∵点E、F分别为AC、BC的中点，

∴EF= AB= ，∴GE+FH=GH﹣EF=4﹣ ，

故答案为：4﹣ ．

根据圆周角和圆心角的关系，求出∠AOB的度数，当GH为⊙O的直径时，GE+FH有最大值；由点E、F分别为AC、BC的中点，根据三角形中位线定理，求出EF的值，得到GE+FH的最大值.