题目内容
 如图,直线L与两坐标轴分别交于A、B点,且OA、OB的长是方程x2-14x+48=0的两根(OA>OB),点C(-6,0)是x轴上一点,点P是直线L上一动点.
如图,直线L与两坐标轴分别交于A、B点,且OA、OB的长是方程x2-14x+48=0的两根(OA>OB),点C(-6,0)是x轴上一点,点P是直线L上一动点.(1)求直线L的解析式.
(2)若点P(x,y)在第三象限内,△OPC的面积记作S,试写出S与x的函数关系式并写出x的取值范围.
分析:(1)解方程x2-14x+48=0得到方程的根,即可求出A、B的坐标,利用待定系数法即可求出函数的解析式;
(2)由于-y是△OPC的高,根据三角形的面积公式解答即可.
(2)由于-y是△OPC的高,根据三角形的面积公式解答即可.
解答:解:(1)解方程x2-14x+48=0得:
(x-6)(x-8)=0,
x1=6,x2=8.
∵OA>OB,
∴A点坐标为(-8,0),B点坐标为(0,6);
设一次函数解析式为y=kx+b,
将(-8,0),(0,6)分别代入解析式得:
,
解得:
;
故函数解析式为y=
x+6.
(2)∵△OPC在第三象限,
∴三角形的高为-y,
则S=
×6×(-y)=-3(
x+6)=-
x-18(x<-8).
(x-6)(x-8)=0,
x1=6,x2=8.
∵OA>OB,
∴A点坐标为(-8,0),B点坐标为(0,6);
设一次函数解析式为y=kx+b,
将(-8,0),(0,6)分别代入解析式得:
|
解得:
|
故函数解析式为y=
| 3 |
| 4 |
(2)∵△OPC在第三象限,
∴三角形的高为-y,
则S=
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
点评:本题考查了解一元一次方程及待定系数法求函数解析式,找到函数与x轴、y轴的交点坐标是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
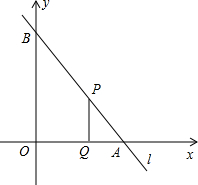 如图,直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OB>OA),P是直线l上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q.
如图,直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OB>OA),P是直线l上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q. OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.
OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.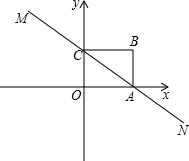 (2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根. (2011•裕华区二模)如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y=
(2011•裕华区二模)如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y= 已知:如图,直线l1与y轴交点坐标为(0,-1),直线l2与x轴交点坐标为(3,0),两直线交点为P(1,1),解答下面问题:
已知:如图,直线l1与y轴交点坐标为(0,-1),直线l2与x轴交点坐标为(3,0),两直线交点为P(1,1),解答下面问题: