题目内容
7、如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠OAD=（ ）分析：根据△OAD≌△OBC得∠OAD=∠OBC，再根据三角形内角和定理求出∠OBC的度数即可．
解答：解：∵△OAD≌△OBC，
∴∠OAD=∠OBC，
∵∠O=65°，∠C=20°，
∴∠OBC=180°-65°-20°=95°，
∴∠OAD=95°
故选D．
∴∠OAD=∠OBC，
∵∠O=65°，∠C=20°，
∴∠OBC=180°-65°-20°=95°，
∴∠OAD=95°
故选D．
点评：此题考查学生对全等三角形的性质和三角形内角定理的理解和掌握，解答此题的关键是根据△OAD≌△OBC得∠OAD=∠OBC．
练习册系列答案
相关题目
7、如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠OAD=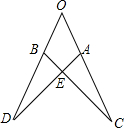
如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠AEC的度数是（ ）
如图，若△OAD≌△OBC，且∠C=20°，则∠D等于（ ）