题目内容
当m分析:由关于x的二次方程mx2-(1-2m)x+m=0没有实数根,得m≠0,且△<0,即△=(1-2m)2-4m2=1-4m<0,解两个不等式可得m的取值范围.
解答:解:当m≠0,且△<0时,关于x的二次方程mx2-(1-2m)x+m=0没有实数根,
∵△=[-(1-2m)]2-4•m•m=1-4m,
∴1-4m<0,即m>
.
故答案为:m>
.
∵△=[-(1-2m)]2-4•m•m=1-4m,
∴1-4m<0,即m>
| 1 |
| 4 |
故答案为:m>
| 1 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的定义.

练习册系列答案
相关题目
 (2013•门头沟区一模)已知关于x的一元二次方程
(2013•门头沟区一模)已知关于x的一元二次方程 已知关于x的一元二次方程
已知关于x的一元二次方程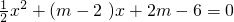 .
.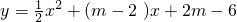 的图象与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,且2AB=3OC,求m的值;
的图象与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,且2AB=3OC,求m的值;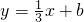 与图象G只有一个公共点时,b的取值范围.
与图象G只有一个公共点时,b的取值范围.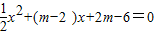 .
.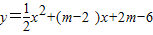 的图象与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,且2AB=3OC,求m的值;
的图象与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,且2AB=3OC,求m的值;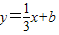 与图象G只有一个公共点时,b的取值范围.
与图象G只有一个公共点时,b的取值范围.