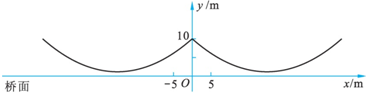
题目内容
如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
(1)钢缆的最低点到桥面的距离是
(2)两条钢缆最低点之间的距离是
(3)右边的抛物线解析式是
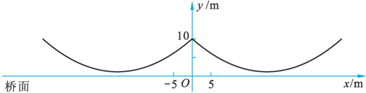
(1)钢缆的最低点到桥面的距离是
1
1
m;(2)两条钢缆最低点之间的距离是
40
40
m;(3)右边的抛物线解析式是
y=0.0225x2-0.9x+10
y=0.0225x2-0.9x+10
.
分析:(1)根据抛物线顶点的坐标公式进行求解,再根据抛物线顶点的纵坐标可得出钢缆的最低点到桥面的距离;
(2)根据两最低点的横坐标可得出两条钢缆最低点之间的距离;
(3)由于两个函数都交于y轴的一点,那么c相等.两个函数的开口方向和开口度在同一直角坐标系中是一样的,所以a相同,a相等,由于两个函数的对称轴关于y轴对称,那么两个函数的b互为相反数.
(2)根据两最低点的横坐标可得出两条钢缆最低点之间的距离;
(3)由于两个函数都交于y轴的一点,那么c相等.两个函数的开口方向和开口度在同一直角坐标系中是一样的,所以a相同,a相等,由于两个函数的对称轴关于y轴对称,那么两个函数的b互为相反数.
解答:解:(1)抛物线的顶点坐标为(-
,
),
∴-
=-
=-20,
=
=1,
故可得左面的一条抛物线的顶点坐标是:(-20,1).
由顶点的纵坐标为1,可得钢缆的最低点到桥面的距离是1米.
故答案为:1;
(2)由两条抛物线的顶点的横坐标为-20、20,
可得两条钢缆最低点之间的距离是:40米.
故答案为:40;
(3)把y=0.0225x2+0.9x+10中的一次项系数0.9变成相反数,得到:
y=0.0225x2-0.9x+10.
故答案为:y=0.0225x2-0.9x+10.
| b |
| 2a |
| 4ac-b2 |
| 4a |
∴-
| b |
| 2a |
| 0.9 |
| 2×0.0225 |
| 4ac-b2 |
| 4a |
| 4×0.0225×10-0.92 |
| 4×0.0225 |
故可得左面的一条抛物线的顶点坐标是:(-20,1).
由顶点的纵坐标为1,可得钢缆的最低点到桥面的距离是1米.
故答案为:1;
(2)由两条抛物线的顶点的横坐标为-20、20,
可得两条钢缆最低点之间的距离是:40米.
故答案为:40;
(3)把y=0.0225x2+0.9x+10中的一次项系数0.9变成相反数,得到:
y=0.0225x2-0.9x+10.
故答案为:y=0.0225x2-0.9x+10.
点评:此题考查了二次函数的应用,解答本题的关键是掌握二次函数的顶点坐标公式,坐标和线段长度之间的转换,综合考查的知识点较多.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
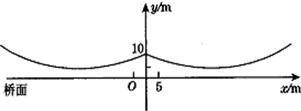
 标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称. 如图所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为
如图所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为