题目内容
【题目】如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
A.5 ![]()
B.10 ![]()
C.10 ![]()
D.15 ![]()
【答案】B
【解析】作点E关于BC的对称点E′,连接E′G交BC于点F,此时四边形EFGH周长取最小值,过点G作GG′⊥AB于点G′,如图所示.
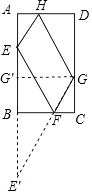
∵AE=CG,BE=BE′,
∴E′G′=AB=10,
∵GG′=AD=5,
∴E′G= ![]() =5
=5 ![]() ,
,
∴C四边形EFGH=2E′G=10 ![]() .
.
所以答案是:B.
【考点精析】关于本题考查的线段的基本性质和矩形的性质,需要了解线段公理:所有连接两点的线中,线段最短.也可简单说成:两点之间线段最短;连接两点的线段的长度,叫做这两点的距离;线段的大小关系和它们的长度的大小关系是一致的;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

练习册系列答案
相关题目
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2(6﹣x) |
(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?