题目内容
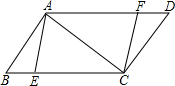 (2013•太原二模)如图,在?ABCD中,AB=6,BC=10,对角线AC⊥AB,点E,F分别是边BC,AD上的点,且BE=DF.
(2013•太原二模)如图,在?ABCD中,AB=6,BC=10,对角线AC⊥AB,点E,F分别是边BC,AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;
(2)填空:
①当BE的长度为
5
5
时,四边形AECF是菱形;②当BE的长度为
3.6
3.6
时,四边形AECF是矩形.分析:(1)首先根据平行四边形的性质可得AD∥BC,AD=BC,再证明AF=EC,可证明四边形AECF是平行四边形;
(2)①根据直角三角形斜边上的中线等于斜边的一半可得AE=
CB=5,然后再根据一组邻边相等的平行四边形是菱形;
②当AE⊥BC时,四边形AECF是矩形,根据勾股定理分别计算出AC长,再计算出AE长,然后再利用勾股定理计算出BE长即可.
(2)①根据直角三角形斜边上的中线等于斜边的一半可得AE=
| 1 |
| 2 |
②当AE⊥BC时,四边形AECF是矩形,根据勾股定理分别计算出AC长,再计算出AE长,然后再利用勾股定理计算出BE长即可.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)解:①当EB=5时,四边形AECF是菱形;
∵AC⊥AB,
∴∠BAC=90°,
∵CB=10,EB=5,
∴E为BC中点,
∴AE=
CB=5,
∴AE=EC,
又∵四边形AECF是平行四边形,
∴四边形AECF是菱形;
故答案为:5.
②当BE=3.6时,四边形AECF是矩形,
当AE⊥BC时,四边形AECF是矩形,
∵AB=6,BC=10,
∴AC=8,
∴
×AB×AC=
×CB×AE,
AE=
,
EB=
=3.6,
故答案为:3.6.
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)解:①当EB=5时,四边形AECF是菱形;
∵AC⊥AB,
∴∠BAC=90°,
∵CB=10,EB=5,
∴E为BC中点,
∴AE=
| 1 |
| 2 |
∴AE=EC,

又∵四边形AECF是平行四边形,
∴四边形AECF是菱形;
故答案为:5.
②当BE=3.6时,四边形AECF是矩形,
当AE⊥BC时,四边形AECF是矩形,
∵AB=6,BC=10,
∴AC=8,
∴
| 1 |
| 2 |
| 1 |
| 2 |
AE=
| 24 |
| 5 |
EB=
| AB2-AE2 |
故答案为:3.6.
点评:此题主要考查了平行四边形、菱形、矩形的判定,关键是掌握各种特殊四边形的判定方法.

练习册系列答案
相关题目
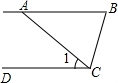 (2013•太原二模)如图,AB∥CD,AC=AB,∠1=40°,则∠B的度数是( )
(2013•太原二模)如图,AB∥CD,AC=AB,∠1=40°,则∠B的度数是( )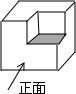 (2013•太原二模)如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )
(2013•太原二模)如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )