题目内容
【题目】已知二次函数
的图像如图，顶点坐标D为（3， 
）。它与
轴交于A，B两点（点A在B的左侧），与
轴交于C点，且AB的长为12. 动点P从A点出发，沿AB方向以1个单位长度/秒的速度向点B运动，设运动时间为t秒.
（1）求二次函数的解析式；
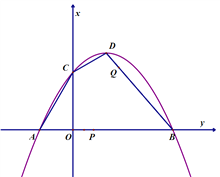
（2）当△PDB为等腰三角形时，求t的值；
（3）若动点Q与P同时从A点出发，点Q沿折线ACCDDB运动，在AC，CD，DB上运动的速度分别为3，
，2 (个单位长度/秒)﹒当P，Q中的一点到达B点时，两点同时停止运动．连结PQ.
①当PQ的中点恰好落在y轴上时，求t的值；
②在P，Q的运动过程中，若线段PQ的垂直平分线与线段BD有交点时，请直接写出t的取值范围.
【答案】（1）
（2）t=5 或
（3）
（4）
或
【解析】试题分析：（1）由顶点坐标（3， 
）可设
，由AB=12及顶点坐标（3， 
），可得a的值，从而求出二次函数的解析式；
（2）分两种情况：PD=PB；BD=BP进行讨论，得出t 值；
试题解析：（1）由题意可知二次函数
又∵AB=12
得
（2）当PD=PB时， 
解得 t=5
当BD=BP时， 
∴
（3）当PQ的中点在y轴上时，过点Q作QE垂直y轴
在RT
中， 
∴
解得
（4）
或
练习册系列答案
阅读快车系列答案
相关题目
