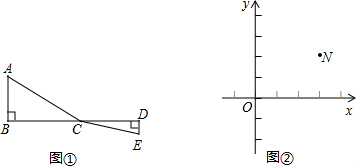
题目内容
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.

1.用含x的代数式表示AC+CE的长
2.请问点C满足什么条件时,AC+CE的值最小?
3.根据(2)中的规律和结论,请构图求出代数式 的最小值.
的最小值.
1.![]()
2.当C点在线段BD与线段AE的交点处的时候,AC+CE的值最小.
3.13
解析:(1)∵![]()
∴

∴ ![]()
(2)当C点在线段BD与线段AE的交点处的时候,AC+CE的值最小.
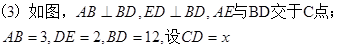

(能正确构图,并且所列线段的长度正确)
过E点作BD的平行线交AB延长线于F点;
由(2)可知代数式![]() 的最小值就是线段AE的长
的最小值就是线段AE的长
在Rt△AFE中,∠AFE=900,AF=AB+DE=3+2=5
EF=BD=12
![]()
∴代数式![]() 的最小值是13
的最小值是13

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
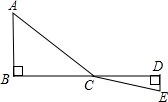 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,则AC+CE的最小值是
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,则AC+CE的最小值是 (2012•青田县模拟)为了探索代数式
(2012•青田县模拟)为了探索代数式 如图,C为线段BD上一点,BC=3,CD=2.△ABC、△ECD均为正三角形,AD交CE于F,则S△ACF:S△DEF的值为( )
如图,C为线段BD上一点,BC=3,CD=2.△ABC、△ECD均为正三角形,AD交CE于F,则S△ACF:S△DEF的值为( )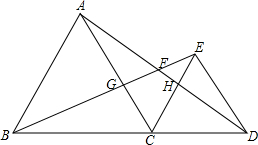 如图,C为线段BD上一点(不与点B,D重合),在BD同侧分别作正三角形ABC和正三角形CDE,AD与BE交于一点F,AD与CE交于点H,BE与AC交于点G.
如图,C为线段BD上一点(不与点B,D重合),在BD同侧分别作正三角形ABC和正三角形CDE,AD与BE交于一点F,AD与CE交于点H,BE与AC交于点G.