��Ŀ����
��ͼ�٣�CΪ�߶�BD��һ���㣬�ֱ����B��D��AB��BD��ED��BD������AC��EC����֪AB=5��DE=1��BD=8����BC=x��
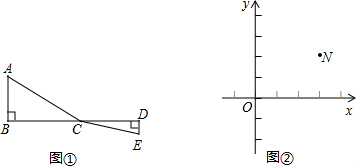
��1����BC�ij�Ϊ����ʱ����C��A��E����ľ�����ȣ�
��2���ú�x�Ĵ���ʽ��ʾAC+CE�ij����ʵ�A��C��E����ʲô����ʱ��AC+CE��ֵ��С��
��3����ͼ�ڣ���ƽ��ֱ������ϵ�У���֪��M��0��4����N��3��2��������ݣ�2���еĹ��ɺͽ��۹�ͼ��x������һ��P��ʹPM+PN��С�������P�����PM+PN����Сֵ��

��1����BC�ij�Ϊ����ʱ����C��A��E����ľ�����ȣ�
��2���ú�x�Ĵ���ʽ��ʾAC+CE�ij����ʵ�A��C��E����ʲô����ʱ��AC+CE��ֵ��С��
��3����ͼ�ڣ���ƽ��ֱ������ϵ�У���֪��M��0��4����N��3��2��������ݣ�2���еĹ��ɺͽ��۹�ͼ��x������һ��P��ʹPM+PN��С�������P�����PM+PN����Сֵ��
��������1������C��A��E����ľ�����ȼ�AC=EC���ɹ��ɶ����������̣��ⷽ�̼��ɣ�
��2�����ڡ�ABC�͡�CDE����ֱ�������Σ���AC��CE���ɹ��ɶ�����ã�����C����AE�������ϣ���������������������֮�ͣ�������֪��AC+CE��AE���ʵ�A��C��E���㹲��ʱ��AC+CE��ֵ��С��
��3��������ֱ��OX�ϵ�ͬ����������M��N����ֱ��OX���е�M��M�ľ���֮����̵ĵ���ڣ�����ͨ����Գ���ȷ��������������һ�����ֱ��OX�ĶԳƵ㣬�ԳƵ�����һ���������OX�Ľ��������Ҫ�ҵ�P�������ù��ɶ������㼴�ɣ�
��2�����ڡ�ABC�͡�CDE����ֱ�������Σ���AC��CE���ɹ��ɶ�����ã�����C����AE�������ϣ���������������������֮�ͣ�������֪��AC+CE��AE���ʵ�A��C��E���㹲��ʱ��AC+CE��ֵ��С��
��3��������ֱ��OX�ϵ�ͬ����������M��N����ֱ��OX���е�M��M�ľ���֮����̵ĵ���ڣ�����ͨ����Գ���ȷ��������������һ�����ֱ��OX�ĶԳƵ㣬�ԳƵ�����һ���������OX�Ľ��������Ҫ�ҵ�P�������ù��ɶ������㼴�ɣ�
����⣺��1����BC=x��BD=8��
��CD=8-x��
��AC=EC��
��x2+52=��8-x��2 +12��
+12��
��ã�x=
��
�൱BC=
ʱ����C��A��E����ľ�����ȣ�
��2��AC+CE=
+
��
��A��C��E��ͬһֱ���ϣ�AC+CE��С��
��3����ͼ��ʾ��P��2��0����
��PM=
=
=2
��
PN=
=
��
��PM+PN��СֵΪ 3
��
��CD=8-x��
��AC=EC��
��x2+52=��8-x��2
 +12��
+12����ã�x=
| 5 |
| 2 |
�൱BC=
| 5 |
| 2 |
��2��AC+CE=
| x2+25 |
| x2-16x+65 |
��A��C��E��ͬһֱ���ϣ�AC+CE��С��
��3����ͼ��ʾ��P��2��0����
��PM=
| OP 2+OM 2 |
| 20 |
| 5 |
PN=
| 1 2+22 |
| 5 |
��PM+PN��СֵΪ 3
| 5 |
�������������������ν�ϵ�˼�룬��ͨ������ֱ�������Σ����ù��ɶ�������������Գ������·�����⣮

��ϰ��ϵ�д�
�����Ŀ
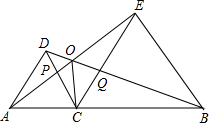
 ��ͼ����CΪ�߶�AB������һ�㣨����A��B�غϣ����ֱ���AC��BCΪһ����AB��ͬ����������ACD�͵�����BCE��CA=CD��CB=CE����ACD���BCE��������ҡ�ACD=��BCE������AE��CD�ڵ�M������BD��CE�ڵ�N��AE��BD���ڵ�P������PC��
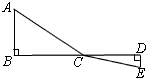
��ͼ����CΪ�߶�AB������һ�㣨����A��B�غϣ����ֱ���AC��BCΪһ����AB��ͬ����������ACD�͵�����BCE��CA=CD��CB=CE����ACD���BCE��������ҡ�ACD=��BCE������AE��CD�ڵ�M������BD��CE�ڵ�N��AE��BD���ڵ�P������PC�� ��ͼ����C���߶�BD�ϣ�AC��BD��CA=CD����E���߶�CA�ϣ�������DE=AB������DE���ӳ���AB�ڵ�F��
��ͼ����C���߶�BD�ϣ�AC��BD��CA=CD����E���߶�CA�ϣ�������DE=AB������DE���ӳ���AB�ڵ�F��
 ����Сֵ��
����Сֵ��