题目内容
【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(4,8).
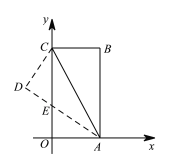
(1)△AEC是等腰三角形吗?请证明;
(2)求点D的横坐标.
【答案】(1)详见解析;(2)D(-![]() ,
,![]() ).
).
【解析】
(1)由翻折可知∠BAC=∠DAC,由OC∥AB可得∠OCA=∠BAC,所以∠EAC=∠ACE,即可证明△AEC是等腰三角形;
(2) 首先过点D作DF⊥OA于F,由四边形OABC是矩形与折叠的性质,易证得△AEC是等腰三角形,然后在Rt△AEO中,利用勾股定理求得AE,OE的长,然后等积求高法得DF的长,利用勾股定理得EF得长,即可得点D的横坐标.
⑴证明:由翻折可知,∠BAC=∠DAC,∵OC∥AB,∴∠OCA=∠BAC,
∴∠EAC=∠ACE,∴AE=CE,即△AEC是等腰三角形.
⑵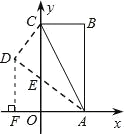
如图,过点D作DF⊥x轴于F,由(1),令AE=CE=x,则OE=8-x,
在Rt△OEA中,由勾股定理,(8-x)2+42=x2,
解得x=5,∴AE=CE=5,OE=DE=3,在Rt△CDE中,由等积求高法,得DF=![]() ,
,
利用勾股定理,EF=![]() ,于是OF=3+
,于是OF=3+![]() =
=![]() ,DF=
,DF=![]() ,
,
∴D(-![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某公司招聘外卖送餐员,送餐员的月工资由底薪1000元加上外卖送单补贴![]() 送一次外卖称为一单
送一次外卖称为一单![]() 构成,外卖送单补贴的具体方案如下:
构成,外卖送单补贴的具体方案如下:
外卖送单数量 | 补贴 |
每月不超过500单 | 6 |
超过500单但不超过m单的部分 | 8 |
超过m单的部分 | 10 |
![]() 若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
![]() 设5月份某“外卖小哥”送餐x单
设5月份某“外卖小哥”送餐x单![]() ,所得工资为y元,求y与x的函数关系式.
,所得工资为y元,求y与x的函数关系式.
![]() 若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.
若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.




