题目内容
先阅读理解,再回答问题.因为
| 12+1 |
| 2 |
| 2 |
| 12+1 |
因为
| 22+2 |
| 6 |
| 6 |
| 22+2 |
因为
| 32+3 |
| 12 |
| 12 |
| 32+3 |
以此类推,我们会发现
| n2+n |
分析:比较被开方数与所给数值的大小,可发现:n2<n2+n<(n+1)2;故
的整数部分为n.
| n2+n |
解答:解:整数部分是n.
理由:∵n为正整数,∴n2<n2+n,
∴n2+n=n(n+1)<(n+1)2,
∴n2<n2+n<(n+1)2,
即n<
<n+1,
∴
的整数部分为n.
理由:∵n为正整数,∴n2<n2+n,
∴n2+n=n(n+1)<(n+1)2,
∴n2<n2+n<(n+1)2,
即n<
| n2+n |
∴
| n2+n |
点评:此题主要考查了无理数的估算能力,解决本题的关键是找到相应的规律;并根据规律得出结论.

练习册系列答案
相关题目
 ,所以
,所以 的整数部分为1;
的整数部分为1; ,所以
,所以 的整数部分为2;
的整数部分为2;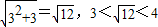 ,所以
,所以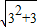 的整数部分为3;
的整数部分为3;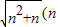 为正整数)的整数部分为 .
为正整数)的整数部分为 . ,所以
,所以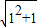 的整数部分为1;
的整数部分为1;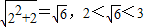 ,所以
,所以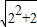 的整数部分为2;
的整数部分为2;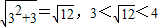 ,所以
,所以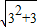 的整数部分为3;
的整数部分为3; 为正整数)的整数部分为 .
为正整数)的整数部分为 .