题目内容
先阅读理解,再回答问题:因为
| 12+1 |
| 2 |
| 2 |
| 12+1 |
因为
| 22+2 |
| 6 |
| 6 |
| 22+2 |
因为
| 32+3 |
| 12 |
| 12 |
| 32+3 |
依此类推,我们不难发现
| n2+n |
分析:应该认真观察已知的几个式子,总结规律,即可求解.
解答:解:∵
的整数部分为1;
的整数部分为2;
的整数部分为3;
∵n2<n2+n<(n+1)2=n2+2n+1,
∴
(n为正整数)的整数部分为n.
| 12+1 |
| 22+2 |
| 32+3 |
∵n2<n2+n<(n+1)2=n2+2n+1,
∴
| n2+n |
点评:此题是探求规律题,需要认真观察,总结规律,不算太难.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 ,所以
,所以 的整数部分为1;
的整数部分为1; ,所以
,所以 的整数部分为2;
的整数部分为2;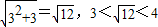 ,所以
,所以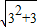 的整数部分为3;
的整数部分为3;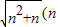 为正整数)的整数部分为 .
为正整数)的整数部分为 . ,所以
,所以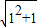 的整数部分为1;
的整数部分为1;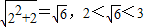 ,所以
,所以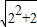 的整数部分为2;
的整数部分为2;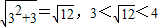 ,所以
,所以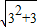 的整数部分为3;
的整数部分为3; 为正整数)的整数部分为 .
为正整数)的整数部分为 .