题目内容
两直线相交于y轴上一点A,分别交x轴与B,C,且两直线互相垂直,若点A坐标为(0,1),B点坐标为(2,0),则点C的坐标为
- A.(
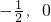 )
) - B.(
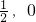 )
) - C.
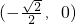
- D.(
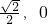 )
)
A
分析:易证△OAB∽△ACB,即可求得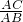 =
=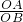 ,已知AB、OA、OB即可求得OC的长,即可解题.
,已知AB、OA、OB即可求得OC的长,即可解题.
解答: 解:∵∠BAC=90°,∠BOA=90°
解:∵∠BAC=90°,∠BOA=90°
∴△OAB∽△ACB,
∴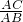 =
=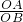 =
= ,
,
∴AC=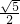 ,
,
故OC= ,
,
∴C点坐标为(- ,0).
,0).
故选A.
点评:本题考查了相似三角形的证明,相似三角形对应边比值相等相等的性质,本题中求证△OAB∽△ACB是解题的关键.
分析:易证△OAB∽△ACB,即可求得
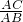 =
=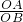 ,已知AB、OA、OB即可求得OC的长,即可解题.
,已知AB、OA、OB即可求得OC的长,即可解题.解答:
 解:∵∠BAC=90°,∠BOA=90°
解:∵∠BAC=90°,∠BOA=90°∴△OAB∽△ACB,
∴
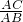 =
=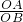 =
= ,
,∴AC=
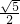 ,
,故OC=
 ,
,∴C点坐标为(-
 ,0).
,0).故选A.
点评:本题考查了相似三角形的证明,相似三角形对应边比值相等相等的性质,本题中求证△OAB∽△ACB是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ∠MOB=
∠MOB=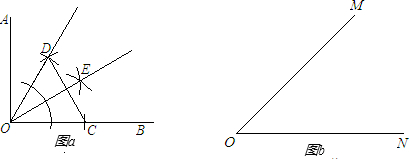
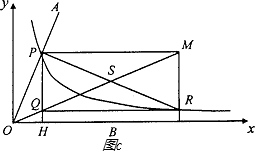

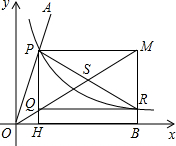
 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: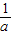 )、R(b,
)、R(b, ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;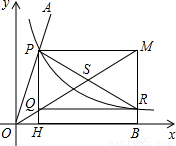
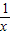 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b,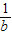 ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;