题目内容
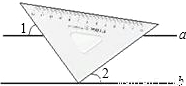
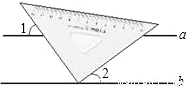
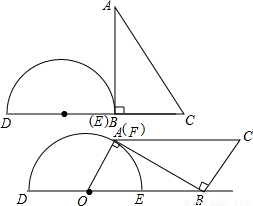
(2010•新疆)如图是一个量角器和一个含30°角的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE.(1)求证:DE∥CF;
(2)当OE=2时,若以O,B,F为顶点的三角形与△ABC相似,求OB的长;
(3)若OE=2,移动三角板ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离.
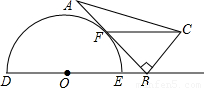
【答案】分析:(1)先作辅助线,连接OF,证明四边形OBCF是平行四边形,得出DE∥CF;
(2)利用相似比求OB的长,
(3)由题意得到点B所在的两个极值位置,求出点B移动的最大距离.
解答:(1)证明:连接OF,
∵AB切半圆O于点F,OF是半径,
∴∠OFB=90°,
∵∠ABC=90°,
∴∠OFB=∠ABC,
∴OF∥BC,
∵BC=OE,OE=OF,
∴BC=OF,
∴四边形OBCF是平行四边形,
∴DE∥CF;
(2)解:若△OBF∽△ACB,
∴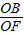 =
=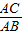 ,
,
∴OB=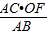 ,
,
∵∠A=30°,∠ABC=90°,BC=OE=2,
∴AC=4,AB=2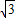 .
.
又∵OF=OE=2,
∴OB=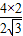 =
= ;
;
若△BOF∽△ACB,
∴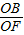 =
=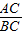 ,
,
∴OB=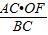 ,
,
∴OB=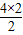 =4;
=4;
综上,OB=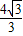 或4;
或4;
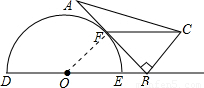
(3)解:画出移动过程中的两个极值图,
由图知:点B移动的最大距离是线段BE的长,
∵∠A=30°,∴∠ABO=30°,∴BO=4,∴BE=2,
∴点B移动的最大距离是线段BE的长为2.
点评:本题利用了平行四边形的判定和性质,切线的性质等知识解决问题.
(2)利用相似比求OB的长,
(3)由题意得到点B所在的两个极值位置,求出点B移动的最大距离.
解答:(1)证明:连接OF,
∵AB切半圆O于点F,OF是半径,
∴∠OFB=90°,
∵∠ABC=90°,
∴∠OFB=∠ABC,
∴OF∥BC,
∵BC=OE,OE=OF,
∴BC=OF,
∴四边形OBCF是平行四边形,
∴DE∥CF;

(2)解:若△OBF∽△ACB,
∴
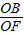 =
=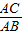 ,
,∴OB=
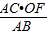 ,
,∵∠A=30°,∠ABC=90°,BC=OE=2,
∴AC=4,AB=2
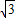 .
.又∵OF=OE=2,
∴OB=
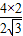 =
= ;
;若△BOF∽△ACB,
∴
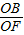 =
=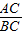 ,
,∴OB=
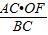 ,
,∴OB=
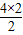 =4;
=4;综上,OB=
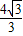 或4;
或4;(3)解:画出移动过程中的两个极值图,
由图知:点B移动的最大距离是线段BE的长,
∵∠A=30°,∴∠ABO=30°,∴BO=4,∴BE=2,
∴点B移动的最大距离是线段BE的长为2.

点评:本题利用了平行四边形的判定和性质,切线的性质等知识解决问题.

练习册系列答案
相关题目