题目内容
【题目】在等边△ABC的外侧作直线BM,点A关于直线BM的对称点为D,连结AD,CD,设CD交直线BM于点E.
(1)依题意补全图1,若∠ABM=30°,求∠BCE的度数;
(2)如图2,若60°<∠ABM<90°,判断直线BM和CD相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由.
【答案】
(1)解:补全的图1如下所示:
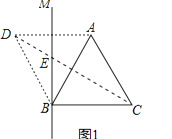
连接BD,如上图1所示,
∵由已知可得,BM垂直平分AD,∠ABM=30°,△ABC是等边三角形,
∴△BDA是等边三角形,AD∥BC且AD=BC,DA=DB,
∴四边形ADBC是菱形,
∵∠ACB=60°,
∴∠BCE=30°;
(2)解:直线BM和CD相交所成的锐角的度数是定值,如下图所示,
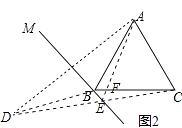
连接AE交BC于点F,
由已知可得,BD=BA,BA=BC,ED=EA,
则∠BDA=∠BAD,∠EDA=∠EAD,BD=BC,
∴∠BDC=∠BCD,∠EDB=∠EAB,
∴∠BCD=∠EAB,
∵∠EFC=∠BFA,∠ABC=60°,
∴∠CEA=∠ABC=60°,
∵∠AEC+∠AEM+∠DEM=180°,∠DEM=∠AEM,
∴∠DEM=60°,
即直线BM和CD相交所成的锐角的度数是定值,这个锐角的度数是60°.
【解析】(1)连接BD,由作图知:BM垂直平分AD根据中垂线定理及等腰三角形的三线合一得出△BDA是等边三角形,由△ABC是等边三角形,故AD∥BC且AD=BC,DA=DB,从而判断出四边形ADBC是菱形,根据菱形的每条对角线平分一组对角得出答案;
(2)直线BM和CD相交所成的锐角的度数是定值,连接AE交BC于点F,根据等边对等角及等量代换得出∠BDA=∠BAD,∠EDA=∠EAD,BD=BC,从而得出∠BDC=∠BCD,∠EDB=∠EAB,根据等量代换得出∠BCD=∠EAB,又由∠AEC+∠AEM+∠DEM=180°,∠DEM=∠AEM,∠CEA=∠ABC=60°,从而得出∠DEM=60°,即直线BM和CD相交所成的锐角的度数是定值,这个锐角的度数是60°.
【考点精析】关于本题考查的角的运算和线段垂直平分线的性质,需要了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案.