题目内容
学以致用问题:任意给定一个矩形,是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半?
讨论:小明说:一定存在.
小华说:一定不存在.
小红说:不一定存在.
探究:老师和大家一起举例说明:(1)如果已知矩形的长和宽和面积分别为7和1,那么它的周长和面积分别16和7,则所求的矩形周长和面积应为8和3.5;
问题转化为:周长为8,面积为3.5的矩形是否存在?
我们假设所求矩形的长为x,固定它的周长为8,则它的宽为______
可列出方程______
解得:______
【答案】分析:设出新矩形的一边长为未知数,根据周长表示出另一边长,根据面积得到方程求解即可.
解答:(1)设所求矩形的长为x,固定它的周长为8,则它的宽为 4-x,
可列出方程 x(4-x)=3.5
解得:x1=2+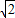 ,x2=2-
,x2=2-
所以:矩形的长为2+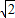 .
.
(2)①如果矩形的长和宽分别为5和1,则矩形的周长为12,面积为5,
∴新矩形的周长为6,面积为2.5.
设所求矩形的长为x,固定它的周长为6,则它的宽为 3-x,
可列出方程 x(3-x)=2.5
△<0,没有实数根
所以不存在这样的矩形;
②由以上两个结论可得小红的说法正确;
故答案为:(1)4-x;x(4-x)=3.5;x1=2+ ,x2=2-
,x2=2-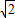 ;矩形的长为2+
;矩形的长为2+ .
.
(2)②小红.
点评:考查一元二次方程在几何图形中的应用;用到的知识点为:矩形的一边长=周长的一半-另一边长.
解答:(1)设所求矩形的长为x,固定它的周长为8,则它的宽为 4-x,
可列出方程 x(4-x)=3.5
解得:x1=2+
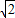 ,x2=2-
,x2=2-
所以:矩形的长为2+
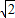 .
.(2)①如果矩形的长和宽分别为5和1,则矩形的周长为12,面积为5,
∴新矩形的周长为6,面积为2.5.
设所求矩形的长为x,固定它的周长为6,则它的宽为 3-x,
可列出方程 x(3-x)=2.5
△<0,没有实数根
所以不存在这样的矩形;
②由以上两个结论可得小红的说法正确;
故答案为:(1)4-x;x(4-x)=3.5;x1=2+
 ,x2=2-
,x2=2-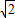 ;矩形的长为2+
;矩形的长为2+ .
.(2)②小红.
点评:考查一元二次方程在几何图形中的应用;用到的知识点为:矩形的一边长=周长的一半-另一边长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
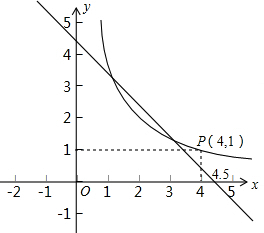 (2012•西城区模拟)探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”
(2012•西城区模拟)探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”