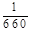题目内容
 世界上著名的莱布尼茨三角形如图所示,则排在第十行的第四个数是
世界上著名的莱布尼茨三角形如图所示,则排在第十行的第四个数是分析:观察不难发现,下一行的第一、二个数的和等于上一行的第一个数,第二、三个数的和为上一行的第二个数,依此类推分别求出第8、9、10行的第一、二、三、四个数,并根据求解方法用上一行的第四个数表示出下一行的第四个数,再写出第四列数的通项公式即可.
解答:解:第8行的第一个数为
,第二个数为
-
=
,第三个数为
-
=
,第四个数为
-
=
,
第9行的第一个数为
,第二个数为
-
=
,第三个数为
-
=
,第四个数为
-
=
,
第10行的第一个数为
,第二个数为
-
=
,第三个数为
-
=
,第四个数为
-
=
,
∵
×
=
,
×
=
,
×
=
,
×
=
,
×
=
,
×
=
,
∴第n行的第四个数为
×(
×
×
×
×
×
×…×
)=
×
=
,
所以,排在第十行的第四个数是
,通项公式第四列通项公式为
.
故答案为:
,
.
| 1 |
| 8 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 56 |
| 1 |
| 42 |
| 1 |
| 56 |
| 1 |
| 168 |
| 1 |
| 105 |
| 1 |
| 168 |
| 1 |
| 280 |
第9行的第一个数为
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 9 |
| 1 |
| 72 |
| 1 |
| 56 |
| 1 |
| 72 |
| 1 |
| 252 |
| 1 |
| 168 |
| 1 |
| 252 |
| 1 |
| 504 |
第10行的第一个数为
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 90 |
| 1 |
| 72 |
| 1 |
| 90 |
| 1 |
| 360 |
| 1 |
| 252 |
| 1 |
| 360 |
| 1 |
| 840 |
∵
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 20 |
| 2 |
| 6 |
| 1 |
| 60 |
| 1 |
| 60 |
| 3 |
| 7 |
| 1 |
| 140 |
| 1 |
| 140 |
| 4 |
| 8 |
| 1 |
| 280 |
| 1 |
| 280 |
| 5 |
| 9 |
| 1 |
| 504 |
| 1 |
| 504 |
| 6 |
| 10 |
| 1 |
| 840 |
∴第n行的第四个数为
| 1 |
| 4 |
| 1 |
| 5 |
| 2 |
| 6 |
| 3 |
| 7 |
| 4 |
| 8 |
| 5 |
| 9 |
| 6 |
| 10 |
| n-4 |
| n |
| 1 |
| 4 |
| 1×2×3×4 |
| n(n-1)(n-2)(n-3) |
| 6 |
| n(n-1)(n-2)(n-3) |
所以,排在第十行的第四个数是
| 1 |
| 840 |
| 6 |
| n(n-1)(n-2)(n-3) |
故答案为:
| 1 |
| 840 |
| 6 |
| n(n-1)(n-2)(n-3) |
点评:本题是对数字变化规律的考查,观察出下一行的相邻的两个与上一行的数的关系是解题的关键,求第四列数的通项时,难点在于观察出用上一行的数表示出下一行的数所乘的分数.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
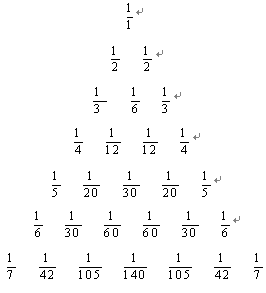
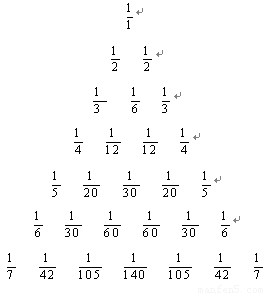
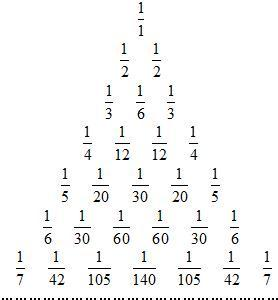 世界上著名的莱布尼茨三角形如图所示,则排在第10行从左边数第3个位置上的数是( )
世界上著名的莱布尼茨三角形如图所示,则排在第10行从左边数第3个位置上的数是( )A、
| ||
B、
| ||
C、
| ||
D、
|
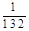 B.
B.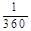 C.
C.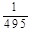 D.
D.