题目内容
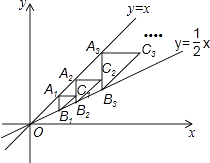
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y= ![]() x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y= ![]() x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示) 
【答案】![]()
【解析】解:∵点A1(2,2),A1B1∥y轴交直线y= ![]() x于点B1 ,
x于点B1 ,
∴B1(2,1)
∴A1B1=2﹣1=1,即△A1B1C1面积= ![]() ×12=
×12= ![]() ;
;
∵A1C1=A1B1=1,
∴A2(3,3),
又∵A2B2∥y轴,交直线y= ![]() x于点B2 ,
x于点B2 ,
∴B2(3, ![]() ),
),
∴A2B2=3﹣ ![]() =
= ![]() ,即△A2B2C2面积=
,即△A2B2C2面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
以此类推,
A3B3= ![]() ,即△A3B3C3面积=
,即△A3B3C3面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
A4B4= ![]() ,即△A4B4C4面积=
,即△A4B4C4面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
…
∴AnBn=( ![]() )n﹣1 , 即△AnBnCn的面积=
)n﹣1 , 即△AnBnCn的面积= ![]() ×[(
×[( ![]() )n﹣1]2=
)n﹣1]2= ![]() .
.
故答案为: ![]()
先根据点A1的坐标以及A1B1∥y轴,求得B1的坐标,进而得到A1B1的长以及△A1B1C1面积,再根据A2的坐标以及A2B2∥y轴,求得B2的坐标,进而得到A2B2的长以及△A2B2C2面积,最后根据根据变换规律,求得AnBn的长,进而得出△AnBnCn的面积即可.本题主要考查了一次函数图象上点的坐标特征以及等腰直角三角形的性质,解决问题的关键是通过计算找出变换规律,根据AnBn的长,求得△AnBnCn的面积.解题时注意:直线上任意一点的坐标都满足函数关系式y=kx+b.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 ![]() =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm